题目内容
已知点A、B的坐标分别为(-1,0),(5,0),直线AM,BM相交于点M,且它们的斜率之积是λ(λ≠0),试讨论点M的轨迹是什么.
【答案】分析:设M的坐标,利用直线AM,BM的斜率之积是λ(λ≠0),建立方程,对λ分类讨论,可得点M的轨迹.
解答:解:设M(x,y),则
∵点A、B的坐标分别为(-1,0),(5,0),
∴kAM=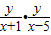
∵直线AM,BM的斜率之积是λ(λ≠0),
∴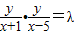
∴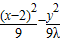 =1
=1
∴λ=-1时,M的轨迹是圆;λ<-1或-1<λ<0时,M的轨迹是椭圆;λ>0时,M的轨迹是双曲线.
点评:本题考查轨迹方程,考查分类讨论的数学思想,属于基础题.
解答:解:设M(x,y),则
∵点A、B的坐标分别为(-1,0),(5,0),
∴kAM=
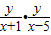
∵直线AM,BM的斜率之积是λ(λ≠0),
∴
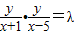
∴
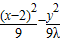 =1
=1∴λ=-1时,M的轨迹是圆;λ<-1或-1<λ<0时,M的轨迹是椭圆;λ>0时,M的轨迹是双曲线.
点评:本题考查轨迹方程,考查分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目