题目内容
已知:如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE·BF·AB=CD3.

证明略
解析:
∵∠ACB=90°,CD⊥AB,
∴CD2=AD·BD,故CD4=AD2·BD2.
又∵Rt△ADC中,DE⊥AC,
Rt△BDC中,DF⊥BC,
∴AD2=AE·AC,BD2=BF·BC.
∴CD4=AE·BF·AC·BC.
又∵AC·BC=AB·CD,
∴CD4=AE·BF·AB·CD,即AE·BF·AB=CD3.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为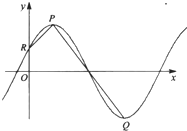 (2013•汕头一模)已知函数.f(x)=Asin(
(2013•汕头一模)已知函数.f(x)=Asin( ,
, ,用a、b表示
,用a、b表示 .
.
 ,
, ,用a、b表示
,用a、b表示 .
.
 已知函数.f(x)=Asin(
已知函数.f(x)=Asin(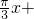 φ),x∈R,A>0,0<φ<
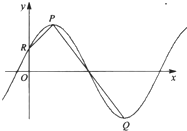
φ),x∈R,A>0,0<φ< ,y=f(x)的部分图象如图所示,点R(0,
,y=f(x)的部分图象如图所示,点R(0, )是该图象上的一点,P,Q分别为该图象在y轴右侧的第一个最高点和第一个最低点,且
)是该图象上的一点,P,Q分别为该图象在y轴右侧的第一个最高点和第一个最低点,且 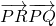 =1.
=1.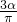 )=
)= ,求cos(2α+
,求cos(2α+ )的値.
)的値.