题目内容
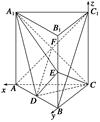
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，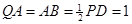
．
（1）证明：平面PQC⊥平面DCQ；
（2）求二面角Q—BP—C的余弦值．
（1）证明过程详见试题解析；（2）二面角Q—BP—C的余弦值为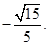
．
解析试题分析：（1）以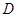
点为中心建立空间坐标系，要证平面
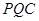⊥平面
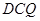，只需证明PQ⊥DQ，PQ⊥DC即可；（2）先求出平面PBC的和平面PBQ的法向量，两个法向量所成的角即为二面角Q—BP—C的平面角，然后求出余弦值即可．
试题解析：（1）依题意有Q（1，1，0），C（0，0，1），P（0，2，0）.
则
所以
即PQ⊥DQ，PQ⊥DC.故PQ⊥平面DCQ.
又PQ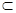
平面PQC，所以平面PQC⊥平面DCQ.
（2）依题意有B（1，0，1），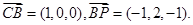
设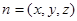
是平面PBC的法向量，则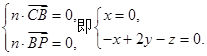
因此可取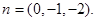
设m是平面PBQ的法向量，则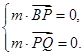
可取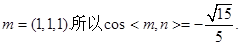
故二面角Q—BP—C的余弦值为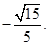
考点：面面垂直的判定定理、二面角的求法、空间坐标系.
练习册系列答案
相关题目
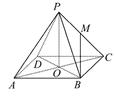
,D是AP的中点，E,G分别为PC,CB的中点，将三角形PCD沿CD折起，使得PD垂直平面ABCD.（1）若F是PD的中点，求证：AP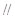
平面EFG;（2）当二面角G-EF-D的大小为
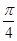时，求FG与平面PBC所成角的余弦值.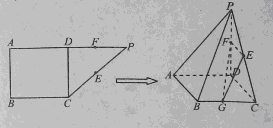
中，底面
是矩形，
平面
，
，
，
是
的中点，
是线段
上的点．
是
的中点时，求证：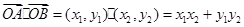
平面
；
的大小为
，试确定
点的位置．
底面ABCD，PD
，
，
．
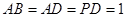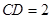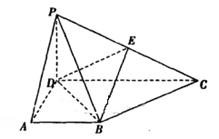
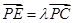，试确定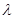
的值，使得二面角E－BD－P的余弦值为
．
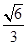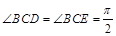，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2.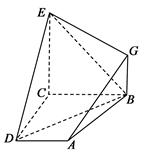
平面BDE;
DE
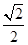AB.
