题目内容
已知向量 ,
, ,
, .
.
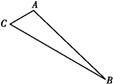
(1)若点 能构成三角形,求实数
能构成三角形,求实数 应满足的条件;
应满足的条件;
(2)若 为直角三角形,且
为直角三角形,且 为直角,求实数
为直角,求实数 的值.
的值.
(1)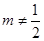 ;(2)
;(2)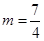 .
.
解析试题分析:(1)根据条件A,B,C,能构成三角形,说明这三点不共线,从反面来考虑,如果A,B,C三点共线,则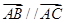 ,由已知条件以及平面向量共线的坐标表示,可以得到
,由已知条件以及平面向量共线的坐标表示,可以得到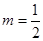 ,故若要使A,B,C三点不共线,则
,故若要使A,B,C三点不共线,则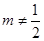 ;(2)根据条件△ABC为直角三角形,且∠A为直角,可得
;(2)根据条件△ABC为直角三角形,且∠A为直角,可得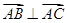 ,根据已知条件与平面向量垂直的坐标表示,可以得到
,根据已知条件与平面向量垂直的坐标表示,可以得到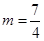 .
.
(1)若点 能构成三角形,则这三点不共线.
能构成三角形,则这三点不共线.
若A,B,C三点共线,则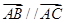 ,
,
又∵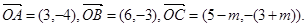
∴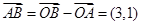 ,
,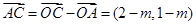 ,∴
,∴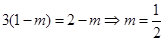 ,
,
∴实数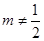 时满足条件. 6分
时满足条件. 6分
(2)∵△ABC为直角三角形,且∠A为直角,则AB⊥AC,即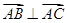
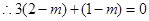 ,解得
,解得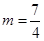 . 12分
. 12分
考点:1.平面向量共线的坐标表示;2.平面向量垂直的坐标表示.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
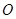 是
是 的三边中垂线的交点,
的三边中垂线的交点,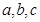 分别为角
分别为角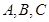 对应的边,已知
对应的边,已知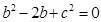 ,则
,则 的范围是_____________.
的范围是_____________. 平面上,点
平面上,点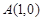 ,点
,点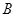 在单位圆上,
在单位圆上,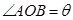 (
(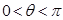 )
)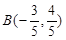 ,求
,求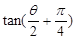 的值;
的值;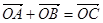 ,四边形
,四边形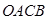 的面积用
的面积用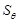 表示,求
表示,求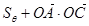 的取值范围.
的取值范围.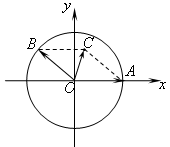
 中,
中, 分别是腰
分别是腰 的中点,
的中点, 在线段
在线段 上,且
上,且 ,下底是上底的2倍,若
,下底是上底的2倍,若 ,用
,用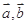 表示
表示 .
.
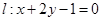 与⊙C:
与⊙C: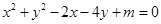 (
(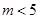 )
)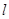 与⊙C相交,求
与⊙C相交,求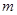 的取值范围。
的取值范围。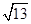 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足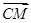 =λ
=λ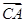 +μ
+μ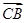 ,且λμ=
,且λμ= .
.
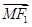 |-|
|-|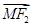 ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由. ,
, ,
, ,其中
,其中 为
为 的内角.
的内角. 的大小;
的大小; ,且
,且 ,求
,求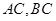 的长.
的长. =-2i+mj,
=-2i+mj, =ni+j,
=ni+j,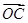 =5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.
=5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.