题目内容
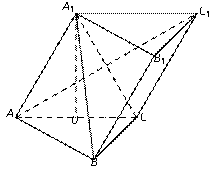
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
(I)求证: AC1⊥平面A1BC;
(II)若AA1=2,求三棱锥C-A1AB的高的大小.
解:
(Ⅰ)因为A1O⊥平面ABC,所以A1O⊥BC.
又BC⊥AC,所以BC⊥平面A1ACC1,所以AC1⊥BC.
因为AA1=AC,所以四边形A1ACC1是菱形,所以AC1⊥A1C.
所以AC1⊥平面A1BC.


(Ⅱ)设三棱锥C-A1AB的高为h.
由(Ⅰ)可知,三棱锥A-A1BC的高为 AC1=
AC1= .
.
因为VC-A1AB=VA-A1BC,即 S△A1ABh=
S△A1ABh= S△A1BC·
S△A1BC· .
.
在△A1AB中,AB=A1B=2 ,AA1=2,所以S△A1AB=
,AA1=2,所以S△A1AB= .
.
在△A1BC中,BC=A1C=2,∠BCA1=90°,所以S△A1BC= BC·A1C=2.
BC·A1C=2.
所以h= .
.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 ≤y≤
≤y≤ ,N=
,N= ≥
≥ ,则表示M∩N的图形面积等于 .
,则表示M∩N的图形面积等于 . 点到
点到 点之间在食堂见面,先到之人等后到之人十五分
点之间在食堂见面,先到之人等后到之人十五分

 满足约束条件
满足约束条件 , 则目标函数
, 则目标函数 的最大值为 .
的最大值为 . .
. 时,恒有
时,恒有 ,求
,求 的最大值;
的最大值; 时,恒有
时,恒有 求
求 的值的程序框图,其中判断框内应填入的是( )
的值的程序框图,其中判断框内应填入的是( ) B.
B. C.
C. D.
D.

 .
. ≤6的解集;
≤6的解集; 的不等式
的不等式 恒成立,求实数
恒成立,求实数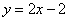 的图象,可以把函数
的图象,可以把函数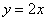 的图象上所有的点
的图象上所有的点 个单位长度
个单位长度