��Ŀ����
14��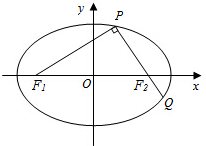 ����ͼ����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2���ҹ�F2��ֱ�߽���Բ��P��Q���㣬��PQ��PF1��
����ͼ����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2���ҹ�F2��ֱ�߽���Բ��P��Q���㣬��PQ��PF1��������|PF1|=2+$\sqrt{2}$��|PF2|=2-$\sqrt{2}$������Բ�ı����̣�
������|PQ|=��|PF1|����$\frac{3}{4}$�ܦˣ�$\frac{4}{3}$����ȷ����Բ������e��ȡֵ��Χ��
���� ��I������Բ�Ķ���ɵã�2a=|PF1|+|PF2|�����a������Բ�İ뽹��Ϊc������PQ��PF1�����ù��ɶ����ɵ�2c=|F1F2|=$\sqrt{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}}$�����c������b2=a2-c2�����ɵó���Բ�ı����̣�
��II����ͼ��ʾ����PQ��PF1��|PQ|=��|PF1|���ɵ�|QF1|=$\sqrt{1+{��}^{2}}|P{F}_{1}|$������Բ�Ķ���ɵã�|PF1|+|PQ|+|QF1|=4a�����|PF1|=$\frac{4a}{1+��+\sqrt{1+{��}^{2}}}$��|PF2|=2a-|PF1|���ɹ��ɶ����ɵã�2c=|F1F2|=$\sqrt{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}}$�����뻯����t=1+��$+\sqrt{1+{��}^{2}}$������ʽ��Ϊe2=$8��\frac{1}{t}-\frac{1}{4}��^{2}+\frac{1}{2}$��������ɣ�
��� �⣺��I������Բ�Ķ���ɵã�2a=|PF1|+|PF2|=��2+$\sqrt{2}$��+��2-$\sqrt{2}$��=4�����a=2��
����Բ�İ뽹��Ϊc����PQ��PF1��
��2c=|F1F2|=$\sqrt{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}}$=$\sqrt{��2+\sqrt{2}��^{2}+��2-\sqrt{2}��^{2}}$=2$\sqrt{3}$��
��c=$\sqrt{3}$��
��b2=a2-c2=1��
����Բ�ı�����Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��II����ͼ��ʾ����PQ��PF1��|PQ|=��|PF1|��
��|QF1|=$\sqrt{|P{F}_{1}{|}^{2}+|PQ{|}^{2}}$=$\sqrt{1+{��}^{2}}|P{F}_{1}|$��
����Բ�Ķ���ɵã�2a=|PF1|+|PF2|=|QF1|+|QF2|��
��|PF1|+|PQ|+|QF1|=4a��
��$��1+��+\sqrt{1+{��}^{2}}��$|PF1|=4a�����|PF1|=$\frac{4a}{1+��+\sqrt{1+{��}^{2}}}$��
|PF2|=2a-|PF1|=$\frac{2a����+\sqrt{1+{��}^{2}}-1��}{1+��+\sqrt{1+{��}^{2}}}$��
�ɹ��ɶ����ɵã�2c=|F1F2|=$\sqrt{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}}$��
��$��\frac{4a}{1+��+\sqrt{1+{��}^{2}}}��^{2}$+$[\frac{2a����+\sqrt{1+{��}^{2}}-1��}{1+��+\sqrt{1+{��}^{2}}}]^{2}$=4c2��
��$\frac{4}{��1+��+\sqrt{1+{��}^{2}}��^{2}}$+$\frac{����+\sqrt{1+{��}^{2}}-1��^{2}}{��1+��+\sqrt{1+{��}^{2}}��^{2}}$=e2��
��t=1+��$+\sqrt{1+{��}^{2}}$������ʽ��Ϊ${e}^{2}=\frac{4+��t-2��^{2}}{{t}^{2}}$=$8��\frac{1}{t}-\frac{1}{4}��^{2}+\frac{1}{2}$��
��t=1+��$+\sqrt{1+{��}^{2}}$����$\frac{3}{4}$�ܦˣ�$\frac{4}{3}$��
��t���ڦ˵�����������3��t��4����$\frac{1}{4}��\frac{1}{t}��\frac{1}{3}$��
��$\frac{1}{2}��{e}^{2}��\frac{5}{9}$�����$\frac{\sqrt{2}}{2}��e��\frac{\sqrt{5}}{3}$��
����Բ�����ʵ�ȡֵ��Χ��$��\frac{\sqrt{2}}{2}��\frac{\sqrt{5}}{3}]$��
���� ���⿼������Բ�Ķ�������̼������ʡ����ɶ���������ʽ�����ʡ�����Ԫ������������������������������������е��⣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�| A�� | ��$\frac{1}{2}$ | B�� | ��$\frac{{\sqrt{2}}}{2}$ | C�� | ��1 | D�� | ��$\sqrt{2}$ |
| A�� | $\frac{25}{2}$ | B�� | $\frac{49}{2}$ | C�� | 12 | D�� | 16 |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
| A�� | 212 | B�� | 211 | C�� | 210 | D�� | 29 |
 ��ͼ����ԲE��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0������������$\frac{{\sqrt{2}}}{2}$����P��0��1���ڶ���CD�ϣ���$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1
��ͼ����ԲE��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0������������$\frac{{\sqrt{2}}}{2}$����P��0��1���ڶ���CD�ϣ���$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1