题目内容
函数y=f(x)是定义域为R的奇函数,且对任意的x∈R,均有f(x+4)=f(x)成立.当x∈(0,2)时,f(x)=-x2+2x+1.(Ⅰ)当x∈[4k-2,4k+2](k∈Z)时,求函数f(x)的表达式;
(Ⅱ)求不等式
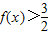 的解集.
的解集.
【答案】分析:(Ⅰ)由f(x+4)=f(x),得出T=4,利用x∈(0,2)时,f(x)=-x2+2x+1.求出当x∈(-2,0)时,
f(x)=x2+2x-1.得出f(x)在一个周期长度上的解析式,再将x∈[4k-2,4k+2]转化为x∈[-2,2]上求解.
(Ⅱ)先求出不等式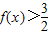 在[-2,2]上的解集,再利用周期性求出所有的结果.
在[-2,2]上的解集,再利用周期性求出所有的结果.
解答:解:(Ⅰ)当x=0时,∵f(0)=-f(0),∴f(0)=0
当x∈(-2,0)时,-x∈(0,2),f(x)=-f(-x)=-(x2-2x+1)=x2+2x-1.
由f(x+4)=f(x)知f(x)为周期函数,且T=4.
当x∈[4k-2,4k)(k∈Z)时,x-4k∈[-2,0),
f(x)=f(x-4k)=(x-4k)2+2(x-4k)-1.
当x∈[4k,4k+2])(k∈Z)时,x-4k∈[0,2],
f(x)=f(x-4k)=-(x-4k)2+2(x-4k)+1.
故当x∈[4k-2,4k+2](k∈Z)时,(x-4k)2+2(x-4k)-1
f(x)=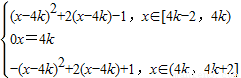
(Ⅱ)当x∈[-2,2]时,由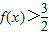 ,得
,得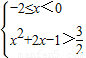 或
或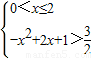
解得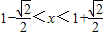 ,因为f(x)是以4为周期的函数,所以不等式
,因为f(x)是以4为周期的函数,所以不等式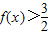 的解集是{x|
的解集是{x|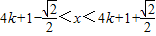 }
}
点评:本题考查函数解析式求解,解不等式.考查转化计算能力.
f(x)=x2+2x-1.得出f(x)在一个周期长度上的解析式,再将x∈[4k-2,4k+2]转化为x∈[-2,2]上求解.
(Ⅱ)先求出不等式
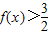 在[-2,2]上的解集,再利用周期性求出所有的结果.
在[-2,2]上的解集,再利用周期性求出所有的结果.解答:解:(Ⅰ)当x=0时,∵f(0)=-f(0),∴f(0)=0
当x∈(-2,0)时,-x∈(0,2),f(x)=-f(-x)=-(x2-2x+1)=x2+2x-1.
由f(x+4)=f(x)知f(x)为周期函数,且T=4.
当x∈[4k-2,4k)(k∈Z)时,x-4k∈[-2,0),
f(x)=f(x-4k)=(x-4k)2+2(x-4k)-1.
当x∈[4k,4k+2])(k∈Z)时,x-4k∈[0,2],
f(x)=f(x-4k)=-(x-4k)2+2(x-4k)+1.
故当x∈[4k-2,4k+2](k∈Z)时,(x-4k)2+2(x-4k)-1
f(x)=
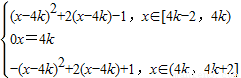
(Ⅱ)当x∈[-2,2]时,由
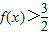 ,得
,得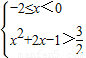 或
或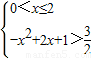
解得
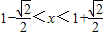 ,因为f(x)是以4为周期的函数,所以不等式
,因为f(x)是以4为周期的函数,所以不等式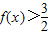 的解集是{x|
的解集是{x|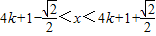 }
}点评:本题考查函数解析式求解,解不等式.考查转化计算能力.

练习册系列答案
相关题目
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.