题目内容
已知椭圆E:
+
=1(a>b>0)经过点A(-2,0),C(1,
)
(1)求椭圆E的方程;
(2)若直线l:x=my+1与椭圆E交于M,N两点,点F为椭圆E的左焦点,当△FMN面积最大时,求此时直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(1)求椭圆E的方程;
(2)若直线l:x=my+1与椭圆E交于M,N两点,点F为椭圆E的左焦点,当△FMN面积最大时,求此时直线l的方程.
分析:(1)把点A、C的坐标代入椭圆方程可得关于a,b的方程组,解出即可;
(2)易判断直线过椭圆的右焦点(1,0),设M(x1,y1),N(x2,y2),则S△FMN=
×2×|y1-y2|=|y1-y2|,联立直线与椭圆的方程消掉x可得y的二次方程,由韦达定理可表示出|y1-y2|,构造函数,利用单调性可得函数的最值,从而可得△FMN面积的最大值及相应的m值;
(2)易判断直线过椭圆的右焦点(1,0),设M(x1,y1),N(x2,y2),则S△FMN=
| 1 |
| 2 |
解答:解:(1)把点A、C的坐标代入椭圆方程可得
,解得
,
所以椭圆E的方程为:
+
=1;
(2)如图所示: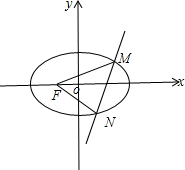
由
得(3m2+4)y2+6my-9=0,
设M(x1,y1),N(x2,y2),
则y1+y2=
,y1y2=
,
易知直线x=my+1过椭圆的右焦点(1,0),
所以S△FMN=
×2×|y1-y2|=
=
=12
=12
,
令t=m2+1(t≥1),则f(t)=9t+
+6,f′(t)=9-
>0,
所以f(t)在[1,+∞)上单调递增,即f(t)≥f(1)=16,
所以S△FMN≤12
=3,即△FMN面积最大为3,此时m=0,
所以所求直线方程为x=1.
|
|
所以椭圆E的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)如图所示:

由
|
设M(x1,y1),N(x2,y2),
则y1+y2=
| -6m |
| 3m2+4 |
| -9 |
| 3m2+4 |
易知直线x=my+1过椭圆的右焦点(1,0),
所以S△FMN=
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
|
|
=12
|
令t=m2+1(t≥1),则f(t)=9t+
| 1 |
| t |
| 1 |
| t2 |
所以f(t)在[1,+∞)上单调递增,即f(t)≥f(1)=16,
所以S△FMN≤12
|
所以所求直线方程为x=1.
点评:本题考查直线与椭圆的位置关系、椭圆的标准方程、韦达定理及三角形面积公式,考查学生分析解决问题的能力,综合性强,运算量大.

练习册系列答案
相关题目

 (2012•佛山二模)已知椭圆E:
(2012•佛山二模)已知椭圆E: