题目内容
已知定义域在R上的单调函数,存在实数x0,使得对于任意的实数x1,x2总有f(x0x1+x0x2)=f(x0)+f(x1)+f(x2)恒成立.
(1)求x0的值;
(2)若f(1)=1,且对于任意的正整数n,有an=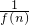 ,bn=f(
,bn=f( )+1
)+1
(Ⅰ)若Sn=a1a2+a2a3+…+anan+1,求Sn;
(Ⅱ)若Tn=b1b2+b2b3+…+bnbn+1,求Tn.
解:(1)令x1=x2=0,得f(0)=f(x0)+2f(0),∴f(x0)=-f(0)①
令x1=1,x2=0,得f(x0)=f(x0)+f(1)+f(0),∴f(1)=-f(0)②
由①②得f(x0)=f(1)
又∵f(x)是单调函数,
∴x0=1
(2)由(1)可得 f(x1+x2)=f(1)+f(x1)+f(x2)+1
则f(n+1)=f(n)+f(1)+1=f(n)+2
又∵f(1)=1
∴f(n)=2n-1 (n∈N*),
∴an=
∴Sn= +
+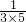 +…+
+…+ =
= (1-
(1- +
+ -
- +…+
+…+ -
- )=
)= (1-
(1- )
)
又∵f(1)=f( +
+ )=f(
)=f( )+f(
)+f( )+f(1),∴f(
)+f(1),∴f( )=0,∴b1=f(
)=0,∴b1=f( )+1=1
)+1=1
∵f( )=f(
)=f( +
+ )=f(
)=f( )+f(
)+f( )+f(1)=2f(
)+f(1)=2f( )+1
)+1
∴bn=f( )+1=2f(
)+1=2f( )+2=2bn+1
)+2=2bn+1
∴ =
=
∴bnbn+1= ×
× =
= ×
×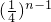
∴Tn=b1b2+b2b3+…+bnbn+1= =
=
分析:(1)利用赋值法,先令 x1=x2=0,再令 x1=1,x2=0,代入已知恒等式即可
(2)令 x1=n,x2=1,代入已知恒等式,即可发现数列{f(n)}为等差数列,从而可用裂项求和的方法求Sn;利用f( )=f(
)=f( +
+ )代入恒等式,即可发现数列{bn}为等比数列,利用等比数列前n项和公式即可求得Tn.
)代入恒等式,即可发现数列{bn}为等比数列,利用等比数列前n项和公式即可求得Tn.
点评:本题考查了函数与数列的综合应用能力,抽象函数表达式的应用,等差等比数列的定义,裂项求和的技巧及等比数列的前n项和公式
令x1=1,x2=0,得f(x0)=f(x0)+f(1)+f(0),∴f(1)=-f(0)②
由①②得f(x0)=f(1)
又∵f(x)是单调函数,
∴x0=1
(2)由(1)可得 f(x1+x2)=f(1)+f(x1)+f(x2)+1
则f(n+1)=f(n)+f(1)+1=f(n)+2
又∵f(1)=1
∴f(n)=2n-1 (n∈N*),
∴an=

∴Sn=
 +
+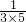 +…+
+…+ =
= (1-
(1- +
+ -
- +…+
+…+ -
- )=
)= (1-
(1- )
)又∵f(1)=f(
 +
+ )=f(
)=f( )+f(
)+f( )+f(1),∴f(
)+f(1),∴f( )=0,∴b1=f(
)=0,∴b1=f( )+1=1
)+1=1∵f(
 )=f(
)=f( +
+ )=f(
)=f( )+f(
)+f( )+f(1)=2f(
)+f(1)=2f( )+1
)+1∴bn=f(
 )+1=2f(
)+1=2f( )+2=2bn+1
)+2=2bn+1∴
 =
=
∴bnbn+1=
 ×
× =
= ×
×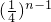
∴Tn=b1b2+b2b3+…+bnbn+1=
 =
=
分析:(1)利用赋值法,先令 x1=x2=0,再令 x1=1,x2=0,代入已知恒等式即可
(2)令 x1=n,x2=1,代入已知恒等式,即可发现数列{f(n)}为等差数列,从而可用裂项求和的方法求Sn;利用f(
 )=f(
)=f( +
+ )代入恒等式,即可发现数列{bn}为等比数列,利用等比数列前n项和公式即可求得Tn.
)代入恒等式,即可发现数列{bn}为等比数列,利用等比数列前n项和公式即可求得Tn.点评:本题考查了函数与数列的综合应用能力,抽象函数表达式的应用,等差等比数列的定义,裂项求和的技巧及等比数列的前n项和公式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目