题目内容
已知命题p1：函数y=2x-2-x在R为增函数，p2：函数y=2x+2-x在R为减函数，则在命题q1：p1∨p2，q2：p1∧p2，q3：（￢p1）和q4：p1∧（￢p2）中，真命题是（ ）A．q1，q3
B．q2，q3
C．q1，q4
D．q2，q4
【答案】分析：先判断命题p1是真命题，P2是假命题，故p1∨p2为真命题，（-p2）为真命题，p1∧（-p2）为真命题．
解答：易知p1是真命题，而对p2：，
当x∈[0，+∞）时，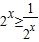
，又ln2＞0，所以y′≥0，函数单调递增；
同理得当x∈（-∞，0）时，函数单调递减，故P2是假命题．
由此可知，q1真，q2假，q3假，q4真．
故选C．
点评：只有p1与P2都是真命题时，p1∧p2才是真命题．只要p1与P2中至少有一个真命题，p1∨p2就是真命题．
解答：易知p1是真命题，而对p2：，
当x∈[0，+∞）时，
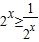，又ln2＞0，所以y′≥0，函数单调递增；同理得当x∈（-∞，0）时，函数单调递减，故P2是假命题．
由此可知，q1真，q2假，q3假，q4真．
故选C．
点评：只有p1与P2都是真命题时，p1∧p2才是真命题．只要p1与P2中至少有一个真命题，p1∨p2就是真命题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
已知命题p1：函数y=2x-2-x在R为增函数，p2：函数y=2x+2-x在R为减函数，则在命题q1：p1∨p2，q2：p1∧p2，q3：（￢p1）∨p2和q4：p1∧（￢p2）中，真命题是（ ）
| A、q1，q3 | B、q2，q3 | C、q1，q4 | D、q2，q4 |