题目内容
①设a,b是两个非零向量,若|a+b|=|a-b|,则a·b =0
②若
③在△ABC中,若 ,则△ABC是等腰三角形
,则△ABC是等腰三角形
④在 中,
中, ,边长a,c分别为a=4,c=
,边长a,c分别为a=4,c= ,则
,则 只有一解。
只有一解。
上面说法中正确的是 .
①②.
解析试题分析:对于①中的式子,两边平方有: ,所以①正确;:对于②有:
,所以①正确;:对于②有: ,因此有
,因此有 ,所以②正确;对于③,根据余弦定理有
,所以②正确;对于③,根据余弦定理有

所以 或
或 ,因此△ABC是等腰三角形或直角三角形,故③不正确;对于④,如图:
,因此△ABC是等腰三角形或直角三角形,故③不正确;对于④,如图:
有 ,所以④不正确.
,所以④不正确.
考点:数量积的运算, ,余弦定理,勾股定理,已知两边和其中一边的对角判断三角形解的个数.
,余弦定理,勾股定理,已知两边和其中一边的对角判断三角形解的个数.

练习册系列答案
相关题目
已知向量 ,
,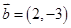 ,若向量
,若向量 满足
满足 ,
, ,则
,则 ="(" )
="(" )
A. | B.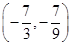 | C. | D. |
在 中,有如下四个命题:
中,有如下四个命题:
① ; ②
; ②
 ;③若
;③若 ,则
,则 为等腰三角形;④若
为等腰三角形;④若 ,则
,则 为锐角三角形.
为锐角三角形.
其中正确的命题序号是
| A.①② | B.①③④ | C.②③ | D.②④ |
已知向量 且
且 ,则
,则 等于
等于
A. | B.- | C. | D.- |
 、
、 满足
满足 ,
, ,且
,且 (
( ),则
),则 .
. 个非零向量
个非零向量 ,且
,且 ,各向量的横坐标和纵坐标均为非负实数,若
,各向量的横坐标和纵坐标均为非负实数,若 (常数),则
(常数),则 的最小值为 .
的最小值为 . ,|
,| +
+ |=|
|=| |,则
|,则 =________.
=________. ="(1,-2),"
="(1,-2),"  ="(a,-1),"
="(a,-1),"  =(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则
=(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则 +
+ 的最小值为 .
的最小值为 .