题目内容
（2013•福建）已知等比数列{an}的公比为q，记bn=am（n-1）+1+am（n-1）+2+…+am（n-1）+m，cn=am（n-1）+1•am（n-1）+2•…•am（n-1）+m，（m，n∈N*），则以下结论一定正确的是（ ）
分析：①bn=am(n-1)(q+q2+…+qm)，当q=1时，bn=mam（n-1），bn+1=mam（n-1）+m=mam（n-1）=bn，此时是常数列，可判断A，B两个选项
②由于等比数列{an}的公比为q，利用等比数列的通项公式可得am(n+1-1)=am(n-1)+m=am(n-1)•qm，cn=
q1+2+…+m=
•q
，得出
即可判断出C，D两个选项．
②由于等比数列{an}的公比为q，利用等比数列的通项公式可得am(n+1-1)=am(n-1)+m=am(n-1)•qm，cn=
| a | m m(n-1) |
| a | m m(n-1) |
| m(m+1) |
| 2 |
| cn+1 |
| cn |
解答：解：①bn=am(n-1)(q+q2+…+qm)，当q=1时，bn=mam（n-1），bn+1=mam（n-1）+m=mam（n-1）=bn，此时是常数列，选项A不正确，选项B正确；
当q≠1时，bn=am(n-1)×
，bn+1=am(n-1)+m•
=am(n-1)qm•
，此时
=qm，选项B不正确，
又bn+1-bn=am(n-1)×
(qm-1)，不是常数，故选项A不正确，
②∵等比数列{an}的公比为q，∴am(n+1-1)=am(n-1)+m=am(n-1)•qm，
∴cn=
q1+2+…+m=
•q
，
∴
=
=
=qm2，故C正确D不正确．
综上可知：只有C正确．
故选C．
当q≠1时，bn=am(n-1)×
| q(qm-1) |
| q-1 |
| q(qm-1) |
| q-1 |
| q(qm-1) |
| q-1 |
| bn+1 |
| bn |
又bn+1-bn=am(n-1)×
| q(qm-1) |
| q-1 |
②∵等比数列{an}的公比为q，∴am(n+1-1)=am(n-1)+m=am(n-1)•qm，
∴cn=
| a | m m(n-1) |
| a | m m(n-1) |
| m(m+1) |
| 2 |
∴
| cn+1 |
| cn |
| ||||
|
| (am(n-1)qm)m | ||
|
综上可知：只有C正确．
故选C．
点评：熟练掌握等差数列与等比数列的定义、通项公式及其前n项和公式是解题的关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
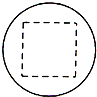（2013•福建）已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、俯视图、均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是