题目内容
如图,棱柱ABCD-A1B(1)求二面角D—A
(2)求点B1到平面A1ADD1的距离.
(3)在直线CC1上是否存在点P,使BP∥平面DA

解:(1)在平面ABCD上,AB=BC=CD=DA=2,
∴四边形ABCD为菱形.
∴BD⊥AC.
∵平面AA
∴BD⊥平面AA
设AC∩BD=O,点O作OE⊥AA1于E点,连结DE,由三垂线定理有AA1⊥DE,
则∠DEO为二面角D—A
在菱形ABCD中,AB=2,∠ABC=60°,
∴AC=AB=BC=2.
∴AO=1,DO=![]() .
.
在Rt△AEO中,OE=AOsinEAO=1·sin60°=![]() ,
,
在Rt△DEO中,tanDEO=![]() =
=![]() =2.
=2.
∴∠DEO=arctan2.
∴二面角D—A
(2)连结A1O、A1B .
由于B1B∥平面A1ADD1.
所以B、B1到平面A1ADD1的距离相等.
设点B到平面A1ADD1的距离等于h.
在△AA1O中,A1O2=A![]() =3.
=3.
∴A1O2+AO2=A
∴A1O⊥AO,而平面AA
∴A1O⊥平面ABCD.
由上述第(1)问有ED⊥A![]() .
.
∴![]() A
A![]() ×2×
×2×![]() =
=![]()
又S△ABD=![]() AO·BD=
AO·BD=![]() ×1×
×1×![]() .
.
由![]() ,有
,有![]()
![]() ·h=
·h=![]() S△ABD·A1O,
S△ABD·A1O,
∴h=![]() ·A1O=
·A1O=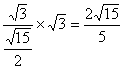 ,
,
即点B1到平面A1ADD1的距离等于![]() .
.
(3)存在这样的点P,连结B
∵A1B1![]() AB
AB![]() DC,
DC,
∴四边形A1B1CD为平行四边形.
∴A1D∥B
在C
∵B1B![]() C
C![]() CP.
CP.
∴四边形BB1CP为平行四边形.
∴BP∥B
则有BP∥平面DA

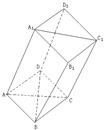 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.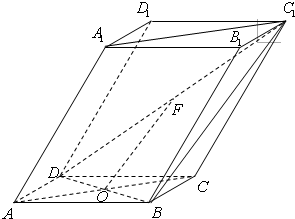 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.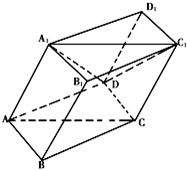 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?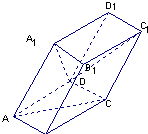 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°