题目内容
15. 如图,设ABCD和ABEF均为平行四边形,他们不在同一平面内,M,N分别为对角线AC,BF上的点,且AM:AC=FN:BF.
如图,设ABCD和ABEF均为平行四边形,他们不在同一平面内,M,N分别为对角线AC,BF上的点,且AM:AC=FN:BF.求证:MN∥平面BEC.
分析 过M作MQ∥BA交CB于点Q,过N作NP∥FE交BE于点P,连接QP,证明四边形MQPN为平行四边形,进而证明出MN∥QP,最后利用线面平行的判定定理证明出结论.
解答  证明:如图示过M作MQ∥BA交CB于点Q,过N作NP∥FE交BE于点P,连接QP,
证明:如图示过M作MQ∥BA交CB于点Q,过N作NP∥FE交BE于点P,连接QP,
在△CAB中,∵MQ∥AB,∴$\frac{CM}{AC}=\frac{MQ}{AB}$,
在△BFE中,同理可得,$\frac{BN}{BF}=\frac{NP}{FE}$,
∵四边形ABFE为平行四边形,∴$AB\underline{\underline{∥}}FE$,
又$\frac{AM}{AC}=\frac{FN}{BF}$,∴$\frac{AC-CM}{AC}=\frac{BF-BN}{BF}$,∴$\frac{CM}{AC}=\frac{BN}{BF}$,∴$\frac{MQ}{AB}=\frac{NP}{FE}$,
∴MQ=NP,
∵$MQ∥AB,NP∥FE,AB\underline{\underline{∥}}FE$,∴MQ∥NP,∴$MQ\underline{\underline{∥}}NP$,
∴四边形MQPN为平行四边形,
∴MN∥QP
又∵MN?面BEC,QP?面BEC,∴MN∥面BEC.
点评 本题主要考查了线面平行的判定定理的运用.解题的关键是证明出MN∥QP,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
3.已知双曲线T:$\frac{{x}^{2}}{4}$-y2=1,过点B(-2,0)的直线交双曲线T于点A(点A不为双曲线顶点),若AB中点Q在直线y=x上,点P为双曲线T上异于A,B的任意一点且不为双曲线的顶点,直线AP,BP分别交直线y=x于M,N两点,则$\overrightarrow{OM}$•$\overrightarrow{ON}$的值为( )
| A. | -$\frac{8}{3}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{1}{2}$ | D. | -8 |
10.直线$y=\sqrt{3}x+2$的倾斜角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
20.若m、n表示直线,α、β表示平面,下列命题正确的是( )
| A. | 若m∥α,α∥β则m∥β | B. | m∥α,m∥n则n∥α | C. | 若m∥α,n⊥α则m⊥n | D. | 若m∥α,n?α则m∥n |
7.已知E={θ|cosθ<sinθ,0≤θ≤2π},F={θ|tanθ<sinθ}.则E∩F为( )
| A. | $(\frac{π}{2},π)$ | B. | $(\frac{π}{4},\frac{3π}{4})$ | C. | $(π,\frac{3π}{2})$ | D. | $(\frac{3π}{4},\frac{5π}{4})$ |
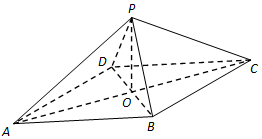 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD⊥BD且AD=BD,AC∩BD=O,PO⊥平面ABCD.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD⊥BD且AD=BD,AC∩BD=O,PO⊥平面ABCD.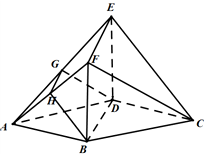 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=2,G和H分别是AE和AF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=2,G和H分别是AE和AF的中点.