题目内容
函数y=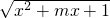
的值域是[0，+∞），则实数m的取值范围是________．
（-∞，-2]∪[2，+∞）
分析：函数y=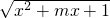的值域是[0，+∞）?当x∈R时，[x2+mx+1]min=0．?方程x2+mx+1=0在实数集范围内有解，解出即可．
解答：∵函数y=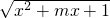的值域是[0，+∞），
∴当x∈R时，[x2+mx+1]min=0．?方程x2+mx+1=0在实数集范围内有解．?△=m2-4≥0，解得m∈（-∞，-2]∪[2，+∞）．
故答案为（-∞，-2]∪[2，+∞）．
点评：对已知问题等价转化是解题的关键．
分析：函数y=
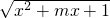的值域是[0，+∞）?当x∈R时，[x2+mx+1]min=0．?方程x2+mx+1=0在实数集范围内有解，解出即可．解答：∵函数y=
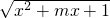的值域是[0，+∞），∴当x∈R时，[x2+mx+1]min=0．?方程x2+mx+1=0在实数集范围内有解．?△=m2-4≥0，解得m∈（-∞，-2]∪[2，+∞）．
故答案为（-∞，-2]∪[2，+∞）．
点评：对已知问题等价转化是解题的关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
的值域是(-∞,0),那么它的定义域是( )
的值域是[0，+∞），则实数m的取值范围是 ．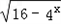
的值域是[0，4）；
x∈R，x2﹣x＞0”的否定是“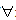
x∈R，x2﹣x≤0”；
的值域是[0，4）；
x∈R，x2﹣x＞0”的否定是“
x∈R，x2﹣x≤0”；