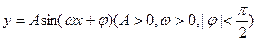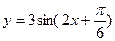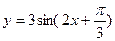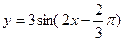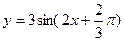题目内容
给出定义在(0,+∞)上的三个函数: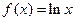 ,
,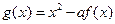 ,
,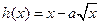 ,已知
,已知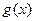 在x=1处取极值.
在x=1处取极值.
(Ⅰ)确定函数h(x)的单调性;
(Ⅱ)求证:当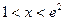 时,恒有
时,恒有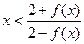 成立;
成立;
(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象,试确定函数y=g(x)-h1(x)的零点个数,并说明理由.
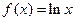 ,
,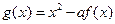 ,
,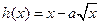 ,已知
,已知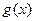 在x=1处取极值.
在x=1处取极值.(Ⅰ)确定函数h(x)的单调性;
(Ⅱ)求证:当
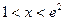 时,恒有
时,恒有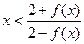 成立;
成立;(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象,试确定函数y=g(x)-h1(x)的零点个数,并说明理由.
(1)h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.(2)见解析 (3)2
(Ⅰ)由题设,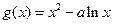 ,则
,则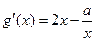 .
.
由已知,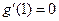 ,即
,即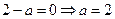 .
.
于是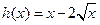 ,则
,则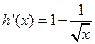 .
.
由 ,所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.
,所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.
(Ⅱ)当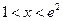 时,
时,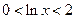 ,即
,即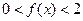 .
.
欲证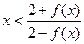 ,只需证
,只需证 ,即证
,即证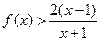 .
.
设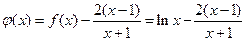 ,则
,则 .
.
当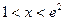 时,
时,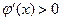 ,所以
,所以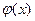 在区间(1,e2)上为增函数.
在区间(1,e2)上为增函数.
从而当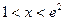 时,
时,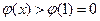 ,即
,即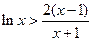 ,故
,故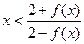 .
.
(Ⅲ)由题设, .令
.令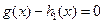 ,则
,则

 ,即
,即 .
.
设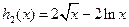 ,
,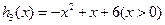 ,则
,则
 ,由
,由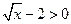 ,得x>4.
,得x>4.
所以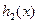 在(4,+∞)上是增函数,在(0,4)上是减函数.
在(4,+∞)上是增函数,在(0,4)上是减函数.
又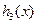 在(0,
在(0, )上是增函数,在(
)上是增函数,在( ,+∞)上是减函数.
,+∞)上是减函数.
因为当x→0时, ,
,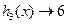 .
.
又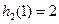 ,
, ,
,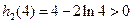 ,
,
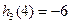 ,则函数
,则函数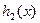 与
与 的大致图象如下:
的大致图象如下:
由图可知,当x>0时,两个函数图象有2个交点,故函数y=g(x)-h1(x)有2个零点.
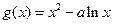 ,则
,则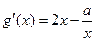 .
. 由已知,
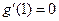 ,即
,即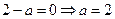 .
. 于是
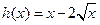 ,则
,则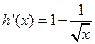 .
. 由
 ,所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.
,所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数. (Ⅱ)当
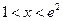 时,
时,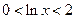 ,即
,即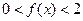 .
. 欲证
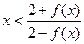 ,只需证
,只需证 ,即证
,即证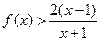 .
. 设
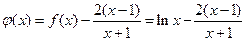 ,则
,则 .
.当
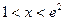 时,
时,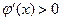 ,所以
,所以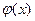 在区间(1,e2)上为增函数.
在区间(1,e2)上为增函数. 从而当
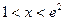 时,
时,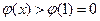 ,即
,即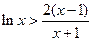 ,故
,故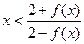 .
. (Ⅲ)由题设,
 .令
.令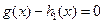 ,则
,则
 ,即
,即 .
. 设
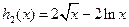 ,
,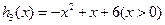 ,则
,则 ,由
,由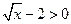 ,得x>4.
,得x>4.所以
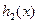 在(4,+∞)上是增函数,在(0,4)上是减函数.
在(4,+∞)上是增函数,在(0,4)上是减函数. 又
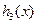 在(0,
在(0, )上是增函数,在(
)上是增函数,在( ,+∞)上是减函数.
,+∞)上是减函数.因为当x→0时,
 ,
,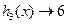 .
.又
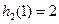 ,
, ,
,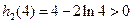 ,
,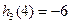 ,则函数
,则函数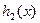 与
与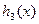 的大致图象如下:
的大致图象如下: 由图可知,当x>0时,两个函数图象有2个交点,故函数y=g(x)-h1(x)有2个零点.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
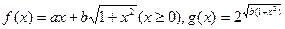 ,且
,且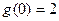 ,
,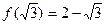 .
.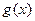 的值域
的值域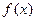 的单调性(不需证明),并求解关于实数
的单调性(不需证明),并求解关于实数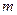 的不等式
的不等式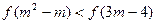 ;
;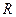 上的函数
上的函数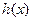 满足
满足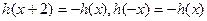 ,且当
,且当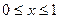 时
时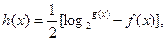 求方程
求方程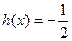 在区间
在区间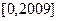 上的解的个数.
上的解的个数. 为偶函数且在区间
为偶函数且在区间 上是单调增函数.
上是单调增函数. 的解析式;
的解析式; ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.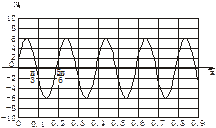
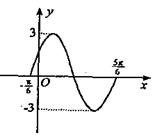
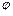 )(A>0,ω>0,|
)(A>0,ω>0,|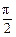 )图象的一部分,试求出其解析式.
)图象的一部分,试求出其解析式.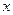 (百台),其总成本为
(百台),其总成本为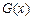 (万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本
(万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本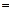 固定成本
固定成本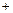 生产成本);销售收入
生产成本);销售收入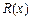 (万元)满足:
(万元)满足: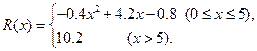 (Ⅰ)要使工厂有盈利,求
(Ⅰ)要使工厂有盈利,求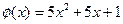
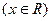 ,函数
,函数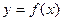 的图象与
的图象与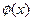 的图象关于点
的图象关于点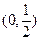 中心对称。
中心对称。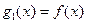 ,
,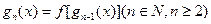 ,试求出使
,试求出使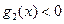 成立的
成立的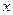 取值范围;
取值范围; ,使
,使 对于区间内的任意实数
对于区间内的任意实数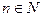 ,且
,且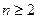 时,都有
时,都有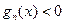 恒成立?
恒成立?