题目内容
在三角形ABC中，角A，B，C所对应的长分别为a，b，c，若a=2，B=
，c=2
，则b=________．
2
分析：由题设条件知，直接利用余弦定理建立方程求出b即可．
解答：由余弦定理可知b2=a2+c2-2accosB=22+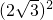
-2×2×2×
=4．
因为b是三角形的边长，所以b=2．
故答案为：2．
点评：本题考查余弦定理的应用，考查计算能力．
分析：由题设条件知，直接利用余弦定理建立方程求出b即可．
解答：由余弦定理可知b2=a2+c2-2accosB=22+
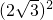-2×2×2×=4．因为b是三角形的边长，所以b=2．
故答案为：2．
点评：本题考查余弦定理的应用，考查计算能力．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，在三角形ABC中，角A，B，C成等差数列，D是BC边的中点，AD=在三角形ABC中，角A、B、C所对的边分别是a、b、c，若a=
b，A=2B，则cosB等于（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|