题目内容
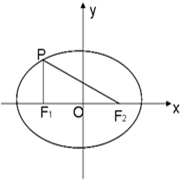 椭圆C:
椭圆C: +
+ =1(a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF2|=
=1(a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF2|= .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l过点M(-2,1),交椭圆C于A,B两点,且M恰是A,B中点,求直线l的方程.
解:(Ⅰ)因为点P在椭圆C上,所以2a=|PF1|+|PF2|=6,a=3.
在Rt△PF1F2中,|F1F2|=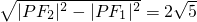 ,故椭圆的半焦距c=
,故椭圆的半焦距c= ,从而b2=a2-c2=4,
,从而b2=a2-c2=4,
所以椭圆C的方程为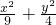 =1.(6分)
=1.(6分)
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).若直线l斜率不存在,显然不合题意.
从而可设过点(-2,1)的直线l的方程为 y=k(x+2)+1,
代入椭圆C的方程得(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称,所以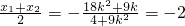 ,解得k=
,解得k= ,
,
所以直线l的方程为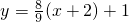 ,即8x-9y+25=0.
,即8x-9y+25=0.
经检验,△>0,所以所求直线方程符合题意. (14分)
分析:(Ⅰ)根据椭圆的定义,可得a的值,在Rt△PF1F2中,|F1F2|=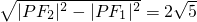 ,可得椭圆的半焦距c=
,可得椭圆的半焦距c= ,从而可求椭圆C的方程为
,从而可求椭圆C的方程为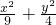 =1;
=1;
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2),设过点(-2,1)的直线l的方程为 y=k(x+2)+1,代入椭圆C的方程,利用A,B关于点M对称,结合韦达定理,即可求得结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,确定椭圆的方程,联立方程是关键.
在Rt△PF1F2中,|F1F2|=
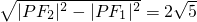 ,故椭圆的半焦距c=
,故椭圆的半焦距c= ,从而b2=a2-c2=4,
,从而b2=a2-c2=4,所以椭圆C的方程为
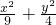 =1.(6分)
=1.(6分)(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).若直线l斜率不存在,显然不合题意.
从而可设过点(-2,1)的直线l的方程为 y=k(x+2)+1,
代入椭圆C的方程得(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称,所以
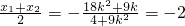 ,解得k=
,解得k= ,
,所以直线l的方程为
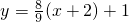 ,即8x-9y+25=0.
,即8x-9y+25=0.经检验,△>0,所以所求直线方程符合题意. (14分)
分析:(Ⅰ)根据椭圆的定义,可得a的值,在Rt△PF1F2中,|F1F2|=
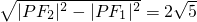 ,可得椭圆的半焦距c=
,可得椭圆的半焦距c= ,从而可求椭圆C的方程为
,从而可求椭圆C的方程为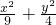 =1;
=1;(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2),设过点(-2,1)的直线l的方程为 y=k(x+2)+1,代入椭圆C的方程,利用A,B关于点M对称,结合韦达定理,即可求得结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,确定椭圆的方程,联立方程是关键.

练习册系列答案
相关题目
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y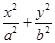 =1(a>b>0)的左、右焦点.
=1(a>b>0)的左、右焦点.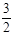 )到点F1、F2的距离之和等于4,求椭圆C的方程;
)到点F1、F2的距离之和等于4,求椭圆C的方程;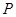 是(Ⅰ)中所得椭圆C上的动点,求线段
是(Ⅰ)中所得椭圆C上的动点,求线段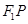 的中点
的中点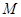 的轨迹方程.
的轨迹方程.