题目内容
设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,![]() )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点P是(1)中所得椭圆上的动点,当P在何位置时,![]() 最大,说明理由,并求出最大值。
最大,说明理由,并求出最大值。
(1)椭圆C的方程为![]() =1,焦点F1(-1,0),F2(1,0 );
=1,焦点F1(-1,0),F2(1,0 );
(2)即![]() 时
时![]() 的最大值为
的最大值为![]()
解析:
(1)椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,
得2a=4,即a=2.
又点A(1,![]() )在椭圆上,因此
)在椭圆上,因此![]() =1得b2=3,于是c2=1.
=1得b2=3,于是c2=1.
所以椭圆C的方程为![]() =1,
=1,
焦点F1(-1,0),F2(1,0)
(2)设![]() ,
,
则![]()
![]() =
=![]() =
=![]()
当且仅当![]() 即
即![]() 时,
时,![]()
![]() 取得最小值
取得最小值![]()
因为![]() 在
在![]() 递减,所以
递减,所以![]() 的最大值为
的最大值为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点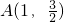 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.