题目内容
(满分12分)
已知函数f ( x )=x 2+ax+b
(1)若f (x)在[ 1,+∞)内递增,求实数a的范围。
(2)若对任意的实数x都有f (1+x)="f" (1-x) 成立,
①求实数 a的值;
②证明函数f(x)在区间[1,+∞ 上是增函数.
上是增函数.
已知函数f ( x )=x 2+ax+b
(1)若f (x)在[ 1,+∞)内递增,求实数a的范围。
(2)若对任意的实数x都有f (1+x)="f" (1-x) 成立,
①求实数 a的值;
②证明函数f(x)在区间[1,+∞
 上是增函数.
上是增函数.① a=-2②略
解:(1)a ≥-2
(2)由f(1+x)=f(1 -x)得,
-x)得,
(1+x)2+a(1+x)+b=(1-x)2+a(1-x)+b,即:(a+2)x=0,
由于对任意的x都成立,∴ a=-2.
a=-2.
可知 f (x)=x 2-2x+b,下面证明函数f(x)在区间[1,+∞ 上是增函数.设
上是增函数.设 ,
,
则 =(
=( )-(
)-( )
)
=( )-2(
)-2( )=(
)=( )(
)( -2)
-2)
∵ ,则
,则 >0,且
>0,且 -2>2-2=0,
-2>2-2=0,
∴ >0,即
>0,即 ,故函数f(x)在区间[1,+∞
,故函数f(x)在区间[1,+∞ 上是增函数.
上是增函数.
法2 :可用导数证明
:可用导数证明
(2)由f(1+x)=f(1
 -x)得,
-x)得,(1+x)2+a(1+x)+b=(1-x)2+a(1-x)+b,即:(a+2)x=0,
由于对任意的x都成立,∴
 a=-2.
a=-2.可知 f (x)=x 2-2x+b,下面证明函数f(x)在区间[1,+∞
 上是增函数.设
上是增函数.设 ,
,则
 =(
=( )-(
)-( )
)=(
 )-2(
)-2( )=(
)=( )(
)( -2)
-2)∵
 ,则
,则 >0,且
>0,且 -2>2-2=0,
-2>2-2=0,∴
 >0,即
>0,即 ,故函数f(x)在区间[1,+∞
,故函数f(x)在区间[1,+∞ 上是增函数.
上是增函数. 法2
 :可用导数证明
:可用导数证明
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
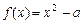 .
. 时,求函数
时,求函数 在区间
在区间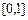 上的最小值;
上的最小值; 时,曲线
时,曲线 在点
在点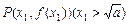 处的切线为
处的切线为 ,
,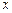 轴交于点
轴交于点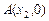
 .
.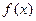 =
=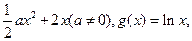
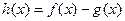 存在单调增区间,求
存在单调增区间,求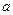 的取值范围;
的取值范围;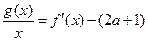 在区间
在区间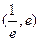 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出 ,把函数
,把函数 的图象向左平移 1个单位,得到函数
的图象向左平移 1个单位,得到函数 的图象, (1)若
的图象, (1)若 为偶函数,求实数
为偶函数,求实数 的值
的值  对于
对于 恒成立,求实数
恒成立,求实数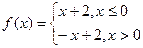 ,则不等式
,则不等式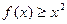 的解集为 。
的解集为 。 的顶点移到
的顶点移到 后,得到的函数的解析式为 .
后,得到的函数的解析式为 . 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则 的取值范围是( )
的取值范围是( )
 ,4]
,4] 在
在 有最大值
有最大值 和最小值
和最小值 ,求
,求 、
、 的值。
的值。 ,
, 是二次函数,若
是二次函数,若 的值域是
的值域是 ,则
,则

