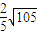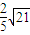题目内容
一个三棱锥的四个顶点均在直径为
的球面上,它的三条侧棱两两垂直,若其中一条侧棱长是另一条侧棱长的2倍,则这3条侧棱长之和的最大值为( )
| 6 |
| A.3 | B.
| C.
| D.
|
设三条弦长分别为x,2x,y,则:x2+(2x)2+y2=6,即:5x2+y2=6,设
x=sinθ,
y=cosθ,
则这3条弦长之和=3x+y=
sinθ+
cosθ=
sin(θ+φ),其中tanφ=
,所以它的最大值为:
.
故选C.
| ||
|
| 1 | ||
|
则这3条弦长之和=3x+y=
3
| ||
|
| 6 |
2
| ||
| 5 |
| ||
| 3 |
| 2 |
| 5 |
| 105 |
故选C.

练习册系列答案
相关题目
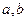 是异面直线,直线
是异面直线,直线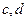 分别与
分别与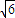 的球面上,它的三条侧棱两两垂直,若其中一条侧棱长是另一条侧棱长的2倍,则这3条侧棱长之和的最大值为( )
的球面上,它的三条侧棱两两垂直,若其中一条侧棱长是另一条侧棱长的2倍,则这3条侧棱长之和的最大值为( )