题目内容
已知f（x）=2sin（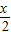
+
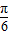）-1，x∈R．（1）求函数f（x）的最小正周期和单调增区间．
（2）函数f（x）的图象可以由函数f（x）=sin
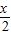（x∈R）的图象经过怎样的变换得到？
【答案】分析：（1）根据正弦函数值域、周期以及单调性的性质进行解答；
（2）按平移的特性“对x轴左移加，右移减；对y轴上移加，下移减”进行变换．
解答：解：
（1）T=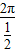
=4π
f（x）=2sin（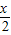
+
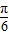）-1的单调增区间满足：
+
∈[
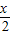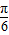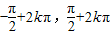]k∈Z
∴f（x）=2sin（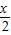
+
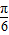）-1的单调增区间x∈[
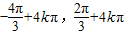]k∈Z
（2）∵f（x）=2sin（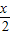
+
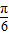）-1=2sin
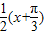-1
根据平移的特性可知：
数f（x）的图象可以由函数f（x）=sin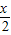
（x∈R）的图象经过左移
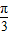，纵坐标扩大原来的2倍，下1个单位得到
点评：考查了三角函数是单调性、周期以及平移特性，属于基础题．
（2）按平移的特性“对x轴左移加，右移减；对y轴上移加，下移减”进行变换．
解答：解：
（1）T=
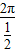=4πf（x）=2sin（
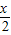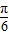+）-1的单调增区间满足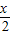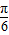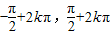：+∈[]k∈Z∴f（x）=2sin（
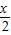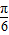+）-1的单调增区间x∈[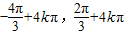]k∈Z（2）∵f（x）=2sin（
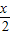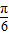+）-1=2sin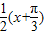-1根据平移的特性可知：
数f（x）的图象可以由函数f（x）=sin
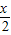（x∈R）的图象经过左移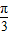，纵坐标扩大原来的2倍，下1个单位得到点评：考查了三角函数是单调性、周期以及平移特性，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
（2011•孝感模拟）已知f（x）=2sin（ωx+φ）的部分图象如图所示，则f（x）的表达式为（ ）