题目内容
P为椭圆C: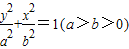 上一点,A、B为圆O:x2+y2=b2上的两个不同的点,直线AB分别交x轴,y轴于M、N两点且
上一点,A、B为圆O:x2+y2=b2上的两个不同的点,直线AB分别交x轴,y轴于M、N两点且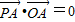 ,
,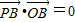 ,O为坐标原点.
,O为坐标原点.(1)若椭圆的准线为
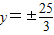 ,并且
,并且 ,求椭圆C的方程.
,求椭圆C的方程.(2)椭圆C上是否存在满足
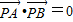 的点P?若存在,求出存在时a,b满足的条件;若不存在,请说明理由.
的点P?若存在,求出存在时a,b满足的条件;若不存在,请说明理由.
【答案】分析:(1)直接根据条件求出PA与PB,进而得到AB的方程,求出M、N两点的坐标,代入 ,可以得到关于a,b的等式;再结合椭圆的准线为
,可以得到关于a,b的等式;再结合椭圆的准线为 ,即可求出a,b的值,进而求出椭圆C的方程.
,即可求出a,b的值,进而求出椭圆C的方程.
(2)先假设存在P(x,y)满足要求,得到OBPA为正方形,即 ,转化为关于点P(x,y)的等式;再结合P(x,y)在椭圆上,即可求出点P(x,y)的坐标所满足的等式,再通过讨论即可得到结论.
,转化为关于点P(x,y)的等式;再结合P(x,y)在椭圆上,即可求出点P(x,y)的坐标所满足的等式,再通过讨论即可得到结论.
解答:解:(1)设A(x1,y1),B(x2,y2),P(x,y)
易求得PA:x1x+y1y=b2,PB:x2x+y2y=b2,
则x1x+y1y=b2,x2x+y2y=b2
于是AB:xx+yy=b2(xy≠0),
可求得


再由条件 ,以及a2-b2=c2易得a=5,b=4,
,以及a2-b2=c2易得a=5,b=4,
于是所求椭圆为 ,
,
(2)设存在P(x,y)满足要求,则当且仅当OBPA为正方形.
 ,即x2+y2=2b2…(1),
,即x2+y2=2b2…(1),
又因为:
解(1)(2)得 ,
,
所以 (ⅰ)当 时,存在P(x,y)满足要求;
时,存在P(x,y)满足要求;
(ⅱ)当 时,不存在P(x,y)满足要求.
时,不存在P(x,y)满足要求.
点评:本题主要考查圆与圆锥曲线的综合问题.圆与圆锥曲线同属于几何内容,都可以用解析法研究(都是二次曲线).所以要特别关注圆与圆锥曲线在一些题目中的交汇、综合.
 ,可以得到关于a,b的等式;再结合椭圆的准线为
,可以得到关于a,b的等式;再结合椭圆的准线为 ,即可求出a,b的值,进而求出椭圆C的方程.
,即可求出a,b的值,进而求出椭圆C的方程.(2)先假设存在P(x,y)满足要求,得到OBPA为正方形,即
 ,转化为关于点P(x,y)的等式;再结合P(x,y)在椭圆上,即可求出点P(x,y)的坐标所满足的等式,再通过讨论即可得到结论.
,转化为关于点P(x,y)的等式;再结合P(x,y)在椭圆上,即可求出点P(x,y)的坐标所满足的等式,再通过讨论即可得到结论.解答:解:(1)设A(x1,y1),B(x2,y2),P(x,y)
易求得PA:x1x+y1y=b2,PB:x2x+y2y=b2,
则x1x+y1y=b2,x2x+y2y=b2
于是AB:xx+yy=b2(xy≠0),
可求得



再由条件
 ,以及a2-b2=c2易得a=5,b=4,
,以及a2-b2=c2易得a=5,b=4,于是所求椭圆为
 ,
,(2)设存在P(x,y)满足要求,则当且仅当OBPA为正方形.
 ,即x2+y2=2b2…(1),
,即x2+y2=2b2…(1),又因为:

解(1)(2)得
 ,
,
所以 (ⅰ)当
 时,存在P(x,y)满足要求;
时,存在P(x,y)满足要求;(ⅱ)当
 时,不存在P(x,y)满足要求.
时,不存在P(x,y)满足要求.点评:本题主要考查圆与圆锥曲线的综合问题.圆与圆锥曲线同属于几何内容,都可以用解析法研究(都是二次曲线).所以要特别关注圆与圆锥曲线在一些题目中的交汇、综合.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 ,点P是椭圆C:
,点P是椭圆C: 上一点,过点P作圆O的两条切线PA、PB,A、B为切点,直线AB分别交
上一点,过点P作圆O的两条切线PA、PB,A、B为切点,直线AB分别交 轴、
轴、 轴于点M、N,则
轴于点M、N,则 的面积的最小值是
的面积的最小值是 B.1 C.
B.1 C. D.
D.
 ,点P是椭圆C:
,点P是椭圆C: 上一点,过点P作圆O的两条切线PA、PB,A、B为切点,直线AB分别交
上一点,过点P作圆O的两条切线PA、PB,A、B为切点,直线AB分别交 轴、
轴、 轴于点M、N,则
轴于点M、N,则 的面积的最小值是( )
的面积的最小值是( ) B.1 C.
B.1 C. D.
D.
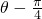 )=3
)=3 .
.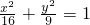 上一点,求P到直线的距离的最大值.
上一点,求P到直线的距离的最大值. )=3
)=3 .
. 上一点,求P到直线的距离的最大值.
上一点,求P到直线的距离的最大值.