题目内容
对于函数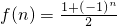 (n∈N*),我们可以发现f(n)有许多性质,如:f(2k)=1(k∈N*)等,下列关于f(n)的性质中一定成立的是
(n∈N*),我们可以发现f(n)有许多性质,如:f(2k)=1(k∈N*)等,下列关于f(n)的性质中一定成立的是
- A.f(n+1)-f(n)=1
- B.f(n+k)=f(n)(k∈N*)
- C.αf(n)=f(n+1)+αf(n)(α≠0)
- D.αf(n+1)=α-(α+1)f(n)(α≠0)
C
分析:对于函数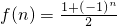 (n∈N*),取一些特殊值n=1,2,3,4,…时观察其函数值的特点,再对选项一一验证即可.
(n∈N*),取一些特殊值n=1,2,3,4,…时观察其函数值的特点,再对选项一一验证即可.
解答:对于函数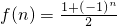 (n∈N*),当n=1,2,3,4,…时的函数值为:0,1,0,1,…
(n∈N*),当n=1,2,3,4,…时的函数值为:0,1,0,1,…
对于A:f(3)-f(2)=-1不成立,故错;
对于B:f(n+1)≠f(n)不成立,故错;
对于C:αf(n)= ,f(n+1)+αf(n)=
,f(n+1)+αf(n)= 成立,故正确;
成立,故正确;
对于D:αf(n+1)=α-(α+1)f(n)(α≠0)不成立,故错;
故选C.
点评:本小题主要考查函数的表示方法、函数周期性的应用、数列的表示方法等基础知识,考查运算求解能力与转化思想.属于基础题.
分析:对于函数
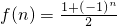 (n∈N*),取一些特殊值n=1,2,3,4,…时观察其函数值的特点,再对选项一一验证即可.
(n∈N*),取一些特殊值n=1,2,3,4,…时观察其函数值的特点,再对选项一一验证即可.解答:对于函数
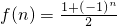 (n∈N*),当n=1,2,3,4,…时的函数值为:0,1,0,1,…
(n∈N*),当n=1,2,3,4,…时的函数值为:0,1,0,1,…对于A:f(3)-f(2)=-1不成立,故错;
对于B:f(n+1)≠f(n)不成立,故错;
对于C:αf(n)=
 ,f(n+1)+αf(n)=
,f(n+1)+αf(n)= 成立,故正确;
成立,故正确;对于D:αf(n+1)=α-(α+1)f(n)(α≠0)不成立,故错;
故选C.
点评:本小题主要考查函数的表示方法、函数周期性的应用、数列的表示方法等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
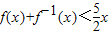 ,定义数列{an},a=8,a1=10,an=f(an-1)(n∈N*).
,定义数列{an},a=8,a1=10,an=f(an-1)(n∈N*).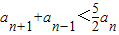 (n∈N*).
(n∈N*).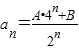 ;
;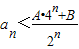 .如果存在,求出A,B的值,如果不存在,说明理由.
.如果存在,求出A,B的值,如果不存在,说明理由.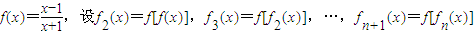 (n∈N*,且n≥2),令集合M={x|f2007(x)=x,x∈R},则集合M为( )
(n∈N*,且n≥2),令集合M={x|f2007(x)=x,x∈R},则集合M为( ) (n∈N*,且n≥2),令集合M={x|f2007(x)=x,x∈R},则集合M为( )
(n∈N*,且n≥2),令集合M={x|f2007(x)=x,x∈R},则集合M为( )