题目内容

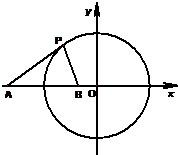
已知直线l与圆O：x2+y2=1在第一象限内相切于点C，并且分别与x，y轴相交于A、B两点，则|AB|的最小值为______．
设直线AB的方程为
x
a
+
y
b
=1，即bx+ay-ab=0
由题意，直线l与圆O相切于第一象限，
∴
ab
a2+b2
=1
又∵
ab
a2+b2
≤
ab
2ab
=
ab
2
（a＞0，b＞0），
∴|AB|=
a2+b2
≥
2ab
≥2
∴a=b时，线段|AB|的最小值为2
故答案为：2．
练习册系列答案
相关题目
圆（x-3）2+（y+4）2=2关于直线x+y=0对称的圆的方程是（　　）
A．.（x+3）2+（y-4）2=2B．.（x-4）2+（y+3）2=2
C．.（x+4）2+（y-3）2=2D．.（x-3）2+（y-4）2=2
对于任意实数a，点P（a，2-a）与圆C：x2+y2=1的位置关系的所有可能是（　　）
A．都在圆内B．都在圆外
C．在圆上、圆外D．在圆上、圆内、圆外
垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程是（　　）
A．x+y-
2
=0		B．x+y+1=0C．x+y-1=0D．x+y+
2
=0
已知圆C：x2+y2=9，点A（-5，0），直线l：x-2y=0．
（1）求与圆C相切，且与直线l垂直的直线方程；
（2）在直线OA上（O为坐标原点），存在定点B（不同于点A），满足：对于圆C上任一点P，都有
PB
PA
为一常数，试求所有满足条件的点B的坐标．
定义：如果一条直线同时与n个圆相切，则称这条直线为这n个圆的公切线．已知有2013个圆Cn：（x-an）2+（y-bn）2=rn2（n=1，2，3，…，2013），其中an ，bn，rn的值由如图程序给出，则这2013个圆的公切线条数（　　）
A．只有一条B．恰好有两条C．有超过两条D．没有公切线
过点P（0，1）向圆x2+y2-4x-6y+12=0引切线，则切线长为______．
若方程x2+y2-2ax+a2+2a-3=0表示圆，且过点A（a，a）可作该圆的两条切线，则实数a的取值范围为______．
设O为坐标原点，C为圆x2+y2-4x+1=0的圆心，圆上有一点M（x，y）满足OM⊥CM，则
y
x
=（　　）
A．
3
3
B．
3
3
或-
3
3
C．
3
D．
3
或-
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网