题目内容
动点M在曲线x2+y2=1上移动,M和定点B(3,0)连线的中点为P,则P点的轨迹方程为:
(2x-3)2+4y2=1
(2x-3)2+4y2=1
.分析:设出M和P点的坐标,利用中点坐标公式把M点的坐标用P点的坐标和常数表示,再由M在定圆上,把M的坐标代入圆的方程整理后即可得到答案.
解答:解:设P点坐标是(x,y),M坐标是(m,n),则有:
2x=3+m,2y=0+n
所以m=2x-3,n=2y
又M在圆上,则有:m2+n2=1.
即P方程是:(2x-3)2+4y2=1.
故答案为(2x-3)2+4y2=1.
2x=3+m,2y=0+n
所以m=2x-3,n=2y
又M在圆上,则有:m2+n2=1.
即P方程是:(2x-3)2+4y2=1.
故答案为(2x-3)2+4y2=1.
点评:本题考查了轨迹方程,考查了利用代入法求曲线的方程,是中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 =(mx,y+1),向量
=(mx,y+1),向量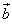 =(x,y-1),
=(x,y-1),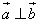 ,动点M(x,y)的轨迹为E,
,动点M(x,y)的轨迹为E,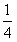 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程;
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程; 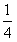 ,设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值。
,设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值。 .证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;
.证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程; .设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
.设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值. .证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;
.证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程; .设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
.设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.