题目内容
设m∈R,在平面直角坐标系中,已知向量 =(mx,y+1),向量
=(mx,y+1),向量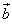 =(x,y-1),
=(x,y-1),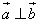 ,动点M(x,y)的轨迹为E,
,动点M(x,y)的轨迹为E,
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知m=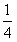 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程;
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程;
(3)已知m=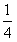 ,设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值。
,设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值。
 =(mx,y+1),向量
=(mx,y+1),向量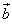 =(x,y-1),
=(x,y-1),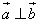 ,动点M(x,y)的轨迹为E,
,动点M(x,y)的轨迹为E,(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知m=
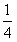 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程;
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求出该圆的方程; (3)已知m=
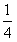 ,设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值。
,设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值。解:(1)因为 ,
,
所以 ,即
,即 ,
,
当m=0时,方程表示两直线,方程为y=±1;
当m=1时,方程表示的是圆;
当m>0且m≠1时,方程表示的是椭圆;
当m<0时,方程表示的是双曲线;
(2)当 时,轨迹E的方程为
时,轨迹E的方程为 ,
,
设圆心在原点的圆的一条切线为y=kx+t,
解方程组 得
得 ,
,
即 ,
,
要使切线与轨迹E恒有两个交点A,B,
则使△= ,
,
即 ,且
,且 ,
,
 ,
,
要使 ,需使
,需使 ,
,
即 ,
,
所以 ,
,
所以又因为直线y=kx+t为圆心在原点的圆的一条切线,
所以圆的半径为 ,
, ,
,
所求的圆为 ;
;
当切线的斜率不存在时,切线为 ,
,
与 交于点
交于点 也满足OA⊥OB;
也满足OA⊥OB;
综上, 存在圆心在原点的圆 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 。
。
(3)当 时,轨迹E的方程为
时,轨迹E的方程为 ,
,
设直线l的方程为y=kx+t,因为直线l与圆C: (1<R<2)相切于A1,
(1<R<2)相切于A1,
由(2)知 , ①
, ①
因为l与轨迹E只有一个公共点B1,
由(2)知 得
得 ,
,
即 有唯一解,
有唯一解,
则△= ,
,
即 , ②
, ②
由①②得 ,此时A,B重合为B1(x1,y1)点,
,此时A,B重合为B1(x1,y1)点,
由 中
中 ,
,
所以, ,
,
B1(x1,y1)点在椭圆上,所以 ,
,
所以 ,
,
在直角三角形OA1B1中,
 ,
,
因为 当且仅当
当且仅当 时取等号,
时取等号,
所以 ,
,
即当 时,|A1B1|取得最大值,最大值为1。
时,|A1B1|取得最大值,最大值为1。
 ,
,所以
 ,即
,即 ,
,当m=0时,方程表示两直线,方程为y=±1;
当m=1时,方程表示的是圆;
当m>0且m≠1时,方程表示的是椭圆;
当m<0时,方程表示的是双曲线;
(2)当
 时,轨迹E的方程为
时,轨迹E的方程为 ,
,设圆心在原点的圆的一条切线为y=kx+t,
解方程组
 得
得 ,
,即
 ,
,要使切线与轨迹E恒有两个交点A,B,
则使△=
 ,
,即
 ,且
,且 ,
, ,
,要使
 ,需使
,需使 ,
,即
 ,
,所以
 ,
,所以又因为直线y=kx+t为圆心在原点的圆的一条切线,
所以圆的半径为
 ,
, ,
,所求的圆为
 ;
;当切线的斜率不存在时,切线为
 ,
,与
 交于点
交于点 也满足OA⊥OB;
也满足OA⊥OB;综上, 存在圆心在原点的圆
 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 。
。 (3)当
 时,轨迹E的方程为
时,轨迹E的方程为 ,
,设直线l的方程为y=kx+t,因为直线l与圆C:
 (1<R<2)相切于A1,
(1<R<2)相切于A1,由(2)知
 , ①
, ① 因为l与轨迹E只有一个公共点B1,
由(2)知
 得
得 ,
,即
 有唯一解,
有唯一解,则△=
 ,
,即
 , ②
, ②由①②得
 ,此时A,B重合为B1(x1,y1)点,
,此时A,B重合为B1(x1,y1)点,由
 中
中 ,
,所以,
 ,
,B1(x1,y1)点在椭圆上,所以
 ,
,所以
 ,
,在直角三角形OA1B1中,
 ,
,因为
 当且仅当
当且仅当 时取等号,
时取等号,所以
 ,
,即当
 时,|A1B1|取得最大值,最大值为1。
时,|A1B1|取得最大值,最大值为1。
练习册系列答案
相关题目
 .证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程;
.证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA⊥OB(O为坐标原点),并求该圆的方程; .设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.
.设直线l与圆C:x2+y2=R2(1<R<2)相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.