Question

【题目】已知一个放置在水平桌面上的密闭直三棱柱容器，如图1，为正三角形，，，里面装有体积为的液体，现将该棱柱绕旋转至图2.在旋转过程中，以下命题中正确的个数是（ ）

①液面刚好同时经过，，三点；

②当平面与液面成直二面角时，液面与水平桌面的距离为；

③当液面与水平桌面的距离为时，与液面所成角的正弦值为.

A.0B.1C.2D.3

Answer 1

【答案】D

【解析】

①若液面刚好同时经过,,三点,则液体的体积为四棱锥,进而求解即可；②当平面与液面成直二面角时,即为图2的位置,画出图形,可先求得液面上方的三棱柱以四边形为底面的高,再与直三棱柱以四边形为底面的高求差即可；③由①可得此时液面与水平桌面的距离为,画出图形,即可求解.

①若液面刚好同时经过,,三点,则液体的体积为四棱锥,

因为,所以①正确；

②当平面与液面成直二面角时,即为图2的位置,设液面与直三棱柱的交点为,如图所示,

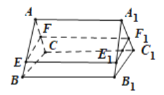
因为直三棱柱的体积为,

所以直棱柱的体积为,

所以,即,则在中边上的高为,

因为在中边上的高为,所以液面与水平桌面的距离为,所以②正确；

③当液面刚好同时经过,,三点时,如图所示,

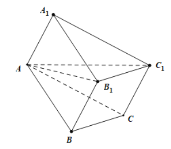
此时,则,

易得,则中边上的高为,

所以,

设点到平面的距离为,则,即,

即液面与水平桌面的距离为,

由棱柱的对称性可得点到平面的距离为,设与液面所成角为,

则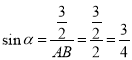,所以③正确,

所以①②③正确,

故选:D