题目内容
已知
且
，函数
在同一坐标系中的图像可能是 
C
解析试题分析：题目中有三种不同的函数图像，我们先从最简单的一次函数开始研究.由A选项可得
.所以相应的对数函数和指数函数都是递减的.从图中可得A选项不成立.同样的B选项中的.所以B选项不成立.C选项符合条件.由D选项可得
.所以另两个函数图像都要递增，从图中可得D选项不成立.故选C.
考点：1.一次函数的性质.2.对数函数的性质.3.指数函数的性质.4.分类、类比的数学思想.
练习册系列答案
相关题目
如图，点
从点
出发，分别按逆时针方向沿周长均为12的正三角形、正方形运动一周，
两点连线的距离
与点P走过的路程
的函数关系分别记为，定义函数
对于函数
，下列结论正确的个数是( )
①
.
②函数
的图象关于直线
对称.
③函数值域为
.
④函数增区间为
.
| A．1 | B．2 | C．3 | D．4 |
下列函数中，既是奇函数又是增函数的为（ ）
A． | B． | C． | D． |
在区间
上不是增函数的是（ ）
A． | B． | C． | D． |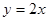
设
是定义在
上的偶函数,且当
时,
.若对任意的
,不等式
恒成立,则实数
的最大值是( )
A． | B． | C． | D．2 |
已知偶函数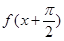
,当
时，
,设
，则( )
A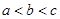． | B． | C． | D． |
．定义域为R的函数
满足
，且当
时，
，则当
时，的最小值为（ ）
A． | B． | C． | D． |
已知
是定义在R上的偶函数,且在
上是增函数,则一定有（ ）
A． | B． ≥ |
C． | D．≤ |
的零点个数为（ ）
| A．4 | B．5 | C．6 | D．7 |