Question

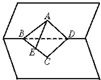
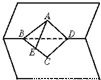
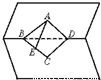
如图：∠BAD=α，∠CAD=β，cosα=

2 5

5

，cosβ=

3 10

10

．
（1）求∠BAC的大小；
（2）当D为BC中点时，判断△ABC的形状，并求

AC

AD

的值．

Answer 1

分析：（1）由sin2α+cos2α=1求出sinα和cosβ，然后由cos∠BAC=cos（α+β）=cosαcosβ-sinαsinβ即可求出角的大小；
（2）由D为BC中点时得出S_△ABD=S_△ACD即可得出得

AB

AC

=

sinβ

sinα

=

2

2

，然后由余弦定理得出AB=BC进而知∠ABC=90°，最后求出AC和AD从而得出答案．

解答：解：（1）由已知，sinα=

1-cos2α

=

5

5

sinβ=

1-cos2β

=

10

10

…（2分）
cos∠BAC=cos（α+β）=cosαcosβ-sinαsinβ=

2 5

5

•

3 10

10

-

5

5

•

10

10

=

2

2

∵∠BAC∈（0，π）∴∠BAC=

π

4

．…（4分）
（2）当D为BC中点时，S_△ABD=S_△ACD，可得

AB

AC

=

sinβ

sinα

=

2

2

，
即AC=

2

AB…（6分）
由余弦定理，BC2=AB2+AC2-2AB•AC•cos

π

4

=3AB2-2AB2=AB2，
即AB=BC，知∠ABC=90°．…（8分）
设AB=BC=2，则AD=

5

，AC=2

2

，所以，

AC

AD

=

2 10

5

．…（12分）

点评：此题考查了两角和与差公式、同角三角函数的基本关系以及三角形的判断，熟练掌握相关公式是解题的关键，属于中档题．