Question

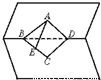
如图，∠BAD=90°的等腰直角三角形ABD与正三角形CBD所在平面互相垂直，E是BC的中点，则AE与平面BCD所成角的大小为______．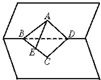

Answer 1

取BD中点F，连AF，EF，CF，设BD=1，
则BE=

1

2

，EF=

1

2

，AB=AD=

2

2

，AF=

1

2

，
由平面ABD⊥平面CBD，AF⊥BD
∴AF⊥平面BCD，
则∠AEF即为AE与平面BCD所成角
在Rt△AEF中，直角边AF=EF
∴∠AEF=45°
即AE与平面BCD所成角的大小为 45°
故答案为：45°．