题目内容
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=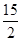 ,求AB的长.
,求AB的长.

解析试题分析:在△ADC中,已知AC=6,AD=5,S△ADC=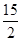 ,
,
则由S△ADC= ·AC·AD·sin∠DAC,求得sin∠DAC=
·AC·AD·sin∠DAC,求得sin∠DAC= ,即∠DAC=30°,
,即∠DAC=30°,
∴ ∠BAC=30°.
而∠ABC=60°,故△ABC为直角三角形.
∵ AC=6,∴ AB= .
.
考点:本小题主要考查三角形面积公式和正弦定理的应用.
点评:解决此类问题的关键是找到合适的三角形,在三角形中利用正弦定理、余弦定理、勾股定理和三角形的面积公式等求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G
 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,AC、BD交于点G.
,AC、BD交于点G.
 ;
; ;
; 的体积.
的体积. 底面
底面 ,且PA=AB.
,且PA=AB.
 平面PAC;
平面PAC; ,∠BCC1=60°.
,∠BCC1=60°.
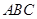 中,
中,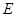 、
、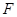 、
、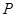 分别是
分别是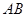 、
、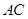 、
、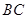 边上的点,满足
边上的点,满足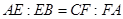
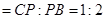 (如图1).将△
(如图1).将△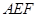 沿
沿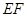 折起到
折起到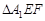 的位置,使二面角
的位置,使二面角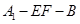 成直二面角,连结
成直二面角,连结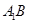 、
、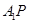 (如图2)
(如图2)
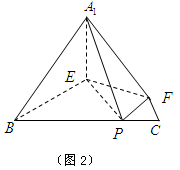
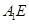 ⊥平面
⊥平面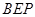 ;
;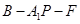 的余弦值.
的余弦值. 中,底面
中,底面 为正三角形,
为正三角形,
 平面ABC,
平面ABC, 的中点,M是线段
的中点,M是线段 上的动点。
上的动点。
 ,请给出证明;
,请给出证明;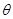 ,求
,求 的最大值。
的最大值。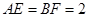 ,
,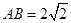 ,现将梯形沿CB、DA折起,使EF//AB且
,现将梯形沿CB、DA折起,使EF//AB且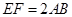 ,得一简单组合体
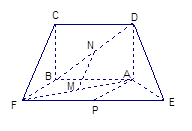
,得一简单组合体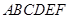 如图(2)所示,已知
如图(2)所示,已知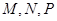 分别为
分别为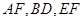 的中点.
的中点.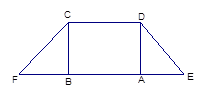
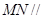 平面
平面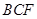 ;
;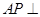 平面
平面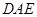 .
.
 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,