题目内容
(本题满分14分)
从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(Ⅰ)求第一次试验恰摸到一个红球和一个白球概率;
(Ⅱ)记试验次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望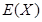 .
.
【答案】
(1) (2)
(2)
【解析】
试题分析:解:(I) ………………4分
………………4分
(II) ;
;  ;
;
 ;
;  ;
;
X的分布列为
|
X |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
……………………12分
 ……………………14分
……………………14分
考点:本试题考查了古典概型和分布列的运用。
点评:对于古典概型的问题,主要是理解试验的基本事件空间,以及事件发生的基本事件空间利用比值来求解概率,结合排列组合的知识得到。而分布列的求解关键是对于各个概率值的求解,属于中档题。

练习册系列答案
相关题目




 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).