题目内容
试求函数y=1+2x-x2(x≥1)和它的反函数的图象的交点.
解:由y=1+2x-x2(x≥1)求得其反函数为y=1+![]() (x≤2),
(x≤2),
由
得1+2x-x2=1+![]() (1≤x≤2),
(1≤x≤2),
即2x-x2=![]() ,
,
则x(2-x)= ![]() ,x(
,x(![]() )2=
)2=![]() ,
,
∴2-x=0或x![]() =1.
=1.
∴x=2或x2(2-x)=1.
由x2(2-x)=1,得2x2-x3=1,
即(x2-1)+(x2-x3)=0,
(x-1)(x+1-x2)=0,
∴x=1或x=![]() .
.
∵1≤x≤2,
∴x=2或x=1或x=![]() .
.
∴y=f(x)和y=f-1(x)的交点有3个,分别是(1,2)、(2,1)、(![]() ,
,![]() ).
).

练习册系列答案
相关题目
 与
与 不共线,若存在非零实数x,y,使得
不共线,若存在非零实数x,y,使得 =
= =-y
=-y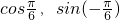 ),
),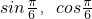 ),且
),且