题目内容
已知椭圆C:
+
=它(a>b>0)的短轴长为2,离心率为
.
(它)求椭圆C的方程;
(2)若过点M(2,0)的引斜率为k的直线与椭圆C相交于两点G、H,设m为椭圆C上一点,且满足
+
=t
(O为坐标原点),当|
-
|<
时,求实数t的取值范围?
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(它)求椭圆C的方程;
(2)若过点M(2,0)的引斜率为k的直线与椭圆C相交于两点G、H,设m为椭圆C上一点,且满足
| OG |
| OH |
| Om |
| mG |
| mH |
2
| ||
| 3 |
(3)∵椭圆C:
+
=3(a>b>r)的短轴长为2,离心率为
,
∴b=3,
=
,
∵a2=b2+c2,
∴a=
,b=3,
∴椭圆C的方程为
+y2=3…(3分)
(2)设G(x3,y3),H(x2,y2),
设直线y=k(x-2),联立椭圆,可得(3+2k2)x2-8kx+8k2-2=r
△=(-8k)2-q(3+2k2)(8k2-2)>r,得k2<
,…(5分)
条件|
-
|<
转换一下就是|
|<
,
∵x3+x2=
,x3x2=
根据弦长公式,
•
<
,得到k2>
.…(3分)
设P(x,y),则
∵
+
=t
,
∴(x3+x2,y3+y2)=t(x,y),
∴x=
(x3+x2),y=
(y3+y2)
根据x3+x2=
,x3x2=
,把x3,x2消成k,得P(
,
)(9分)
然后代入椭圆,得到关系式t2=
,…(33分)
∴t2=
,
∵
<k2<
,
∴实数t的取值范围为(-2,-
)∪(
,2)…(33分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴b=3,
| c |
| a |
| ||
| 2 |
∵a2=b2+c2,
∴a=
| 2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)设G(x3,y3),H(x2,y2),
设直线y=k(x-2),联立椭圆,可得(3+2k2)x2-8kx+8k2-2=r
△=(-8k)2-q(3+2k2)(8k2-2)>r,得k2<
| 3 |
| 2 |
条件|
| PG |
| PH |
2
| ||
| 3 |
| GH |
2
| ||
| 3 |
∵x3+x2=
| 8k |
| 3+2k2 |
| 8k2-2 |
| 3+2k2 |
根据弦长公式,
| 3+k2 |
(
|
2
| ||
| 3 |
| 3 |
| q |
设P(x,y),则
∵
| OG |
| OH |
| OP |
∴(x3+x2,y3+y2)=t(x,y),
∴x=
| 3 |
| t |
| 3 |
| t |
根据x3+x2=
| 8k |
| 3+2k2 |
| 8k2-2 |
| 3+2k2 |
| 8k2 |
| t(3+2k2) |
| -qk |
| t(3+2k2) |
然后代入椭圆,得到关系式t2=
| 3qk2 |
| 3+2k2 |
∴t2=
| 3q | ||
|
∵
| 3 |
| q |
| 3 |
| 2 |
∴实数t的取值范围为(-2,-
2
| ||
| 3 |
2
| ||
| 3 |

练习册系列答案
相关题目
 的直径
的直径 ,
, 是
是 延长线上一点,
延长线上一点, ,割线
,割线 交圆
交圆 ,
, ,过点
,过点 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线 于点
于点 .
. ;
; 的值.
的值.
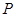 是
是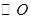 外一点,
外一点,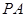 是切线,
是切线, 为切点,割线
为切点,割线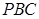 与
与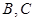 ,
,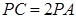 ,
,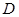 为
为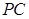 的中点,
的中点,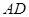 的延长线交
的延长线交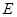 .证明:
.证明: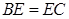 ;
;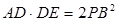
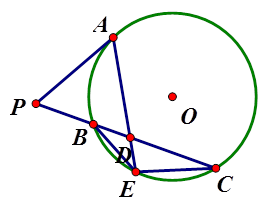


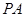 是圆
是圆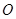 的切线,切点为
的切线,切点为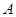 ,
,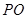 交圆
交圆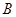 、
、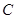 两点,且
两点,且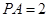 ,
,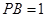 ,则
,则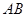 的长为 .
的长为 .