题目内容
已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,若存在
,若存在![]() ,使得
,使得
![]() 成立,求实数b的取值范围.
成立,求实数b的取值范围.
Ⅰ)当![]() 时,
时,![]()
![]() ……………………1分
……………………1分
![]()
![]() ……………………………………….…2分
……………………………………….…2分
所以曲线![]() 在点
在点![]() 处的切线方程
处的切线方程![]() …………………………….…3分
…………………………….…3分
(Ⅱ)![]() ……………4分
……………4分
① 当![]() 时,解
时,解![]() ,得
,得![]() ,解
,解![]() ,得
,得![]()
所以函数![]() 的递增区间为
的递增区间为![]() ,递减区间为在
,递减区间为在![]() ……………………5分
……………………5分
② ![]() 时,令
时,令![]() 得
得![]() 或
或![]()
i)当![]() 时,
时,![]()
| x | |
|
|
|
|
| f’(x) | + | - | + | ||
| f(x) | 增 | 减 | 增 |
……………………6分
函数![]() 的递增区间为
的递增区间为![]() ,
,![]() ,递减区间为
,递减区间为![]() ……………………7分
……………………7分
ii)当![]() 时,
时,![]()
在![]() 上
上![]() ,在
,在![]() 上
上![]() ………………………8分
………………………8分
函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() ………………………9分
………………………9分
(Ⅲ)由(Ⅱ)知,当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]() , ………………………………11分
, ………………………………11分
存在![]() ,使
,使![]() 即存在
即存在![]() ,使
,使![]() ,
,
方法一:只需函数![]() 在[1,2]上的最大值大于等于
在[1,2]上的最大值大于等于![]()
所以有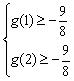 即
即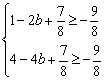 解得:
解得:![]() …………13分
…………13分
方法二:将![]() 整理得
整理得![]()
![]()
从而有![]() 所以
所以![]() 的取值范围是
的取值范围是![]() . …………..13分
. …………..13分

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|