题目内容
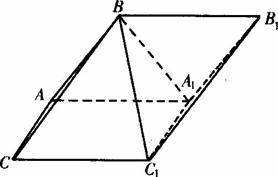
 如图,斜三棱柱A1B1C1-ABC中,侧面AA1C1C⊥底面ABC,侧面AA1C1C是菱形,∠A1AC=60o,E、F分别是A1C1、AB的中点.求证:(1)EF∥平面BB1C1C;(2)平面CEF⊥平面ABC.
如图,斜三棱柱A1B1C1-ABC中,侧面AA1C1C⊥底面ABC,侧面AA1C1C是菱形,∠A1AC=60o,E、F分别是A1C1、AB的中点.求证:(1)EF∥平面BB1C1C;(2)平面CEF⊥平面ABC.分析:(1)取BC中点M,连接FM,C1M,证明FM
AC,推出四边形EFMC1为平行四边形,然后证明EF∥平面BB1C1C;
(2)在平面AA1C1C内,作A1O⊥AC,O为垂足,证明OC
A1E,得到EC
A1O1,证明A1O⊥底面ABC.得到平面CEF⊥平面ABC.
| ∥ |
. |
| 1 |
| 2 |
(2)在平面AA1C1C内,作A1O⊥AC,O为垂足,证明OC
| ∥ |
. |
| ∥ |
. |
解答: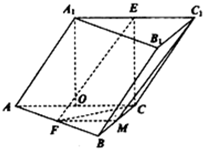 证明:(1)取BC中点M,连接FM,C1M,
证明:(1)取BC中点M,连接FM,C1M,
在△ABC中,因为F,M分别为BA、BC的中点,
所以FM
AC,
因为E为A1C1的中点,AC
A1C1,
所以EF∥EC1,又FM∥A1C1从而四边形EFMC1为平行四边形,
所以EF∥C1M,又因为C1M?平面BB1C1C,EF?平面BB1C1C,
EF∥平面BB1C1C;
(2)在平面AA1C1C内,作A1O⊥AC,O为垂足,
因为∠A1AC=60°,所以AO=
AA1=
AC,
从而O为AC的中点.
所以OC
A1E,因而EC
A1O1,
因为侧面AA1C1C⊥底面ABC,交线为AC,
A1O⊥AC,所以A1O⊥底面ABC.
所以EC⊥底面ABC,
又因为EC?平面EFC,
所以平面CEF⊥平面ABC.
 证明:(1)取BC中点M,连接FM,C1M,
证明:(1)取BC中点M,连接FM,C1M,在△ABC中,因为F,M分别为BA、BC的中点,
所以FM
| ∥ |
. |
| 1 |
| 2 |
因为E为A1C1的中点,AC
| ∥ |
. |
所以EF∥EC1,又FM∥A1C1从而四边形EFMC1为平行四边形,
所以EF∥C1M,又因为C1M?平面BB1C1C,EF?平面BB1C1C,
EF∥平面BB1C1C;
(2)在平面AA1C1C内,作A1O⊥AC,O为垂足,
因为∠A1AC=60°,所以AO=
| 1 |
| 2 |
| 1 |
| 2 |
从而O为AC的中点.
所以OC
| ∥ |
. |
| ∥ |
. |
因为侧面AA1C1C⊥底面ABC,交线为AC,
A1O⊥AC,所以A1O⊥底面ABC.
所以EC⊥底面ABC,
又因为EC?平面EFC,
所以平面CEF⊥平面ABC.
点评:本小题主要考查空间线面关系,考查直线与平面平行,平面与平面垂直的证明,考查空间想像能力和推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
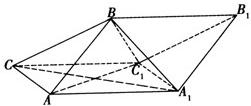 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为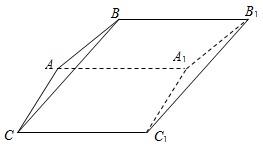 如图,斜三棱柱ABC-A1B1C1中,面AA1C1C是菱形,∠ACC1=60°,侧面ABB1A1⊥AA1C1C,A1B=AB=AC=1.求证:
如图,斜三棱柱ABC-A1B1C1中,面AA1C1C是菱形,∠ACC1=60°,侧面ABB1A1⊥AA1C1C,A1B=AB=AC=1.求证: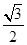 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA1C1C,且A1B=AB=AC=1.
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA1C1C,且A1B=AB=AC=1.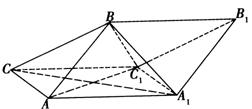
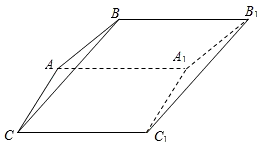 如图,斜三棱柱ABC-A1B1C1中,面AA1C1C是菱形,∠ACC1=60°,侧面ABB1A1⊥AA1C1C,A1B=AB=AC=1.
如图,斜三棱柱ABC-A1B1C1中,面AA1C1C是菱形,∠ACC1=60°,侧面ABB1A1⊥AA1C1C,A1B=AB=AC=1.