题目内容
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D.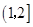 |
A
解析试题分析:为使函数有意义,须 ,解得
,解得
 ,故选A。
,故选A。
考点:本题主要考查求函数定义域的方法,对数函数的性质。
点评:基础题,求函数的定义域,往往要建立不等式组,依据是“分母不为0,偶次根号下式子不小于0,对数的真数大于0”等等。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在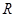 上的奇函数
上的奇函数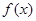 满足
满足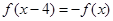 ,且在
,且在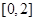 上单调递增,则
上单调递增,则
A.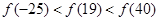 | B.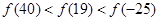 |
C.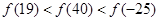 | D.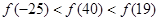 |
已知函数
 .若数列
.若数列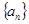 满足
满足 且
且
 ,则实数
,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
已知函数 在
在 上两个零点,则
上两个零点,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
函数 的定义域为( )
的定义域为( )
A. | B. |
C. | D. 或 或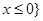 |
已知f(x)是定义在(0,+ )上的非负可导函数,且满足
)上的非负可导函数,且满足 。对任意正数a、b,若a<b,则必有( )
。对任意正数a、b,若a<b,则必有( )
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D. bf(b)≤f(a) |
设函数f (x)是(- ,+
,+ )上的减函数,又若a
)上的减函数,又若a R,则( )
R,则( )
| A.f (a)>f (2a) | B.f (a2)<f (a) |
| C.f (a2+a)<f (a) | D.f (a2+1) <f (a) |
函数 的单调递减区间是( )
的单调递减区间是( )
A. ,+∞) ,+∞) | B.(-∞, | C.(0, | D.[e,+∞) |
下列各图中,可表示函数y=f(x)的图象的只可能是( )
A. | B. |
C. | D. |