题目内容
已知函数 (其中
(其中 为常数且
为常数且 )在
)在 处取得极值.
处取得极值.
(I) 当 时,求
时,求 的单调区间;(II) 若
的单调区间;(II) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
(I)因为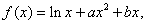 所以
所以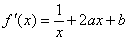 ………………2分
………………2分
因为函数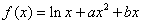 在
在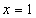 处取得极值
处取得极值
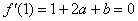 ………………3分
………………3分
当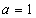 时,
时,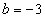 ,
,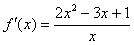 ,
,
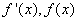 随
随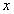 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
|
| 极大值 |
| 极小值 |
|
所以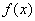 的单调递增区间为
的单调递增区间为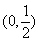 ,
,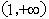 单调递减区间为
单调递减区间为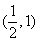 ………………6分
………………6分
(II)因为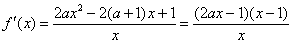
令 ,
,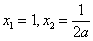 ………………7分
………………7分
因为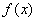 在
在 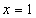 处取得极值,所以
处取得极值,所以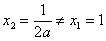
当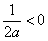 时,
时,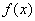 在
在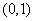 上单调递增,在
上单调递增,在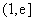 上单调递减
上单调递减
所以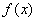 在区间
在区间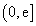 上的最大值为
上的最大值为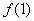 ,令
,令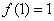 ,解得
,解得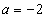 ………………9分
………………9分
当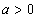 ,
,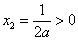
当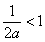 时,
时,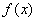 在
在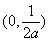 上单调递增,
上单调递增,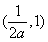 上单调递减,
上单调递减,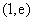 上单调递增
上单调递增
所以最大值1可能在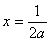 或
或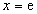 处取得
处取得
而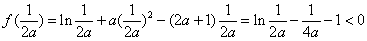
所以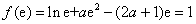 ,解得
,解得 ………………11分
………………11分
当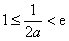 时,
时,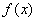 在区间
在区间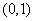 上单调递增,
上单调递增,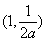 上单调递减,
上单调递减,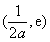 上单调递增
上单调递增
所以最大值1可能在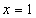 或
或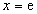 处取得
处取得
而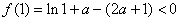 所以
所以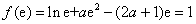 ,
,
解得 ,与
,与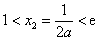 矛盾………………12分
矛盾………………12分
当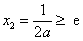 时,
时,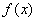 在区间
在区间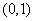 上单调递增,在
上单调递增,在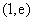 单调递减,
单调递减,
所以最大值1可能在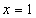 处取得,而
处取得,而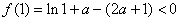 ,矛盾
,矛盾
综上所述,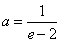 或
或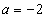

练习册系列答案
相关题目








 是函数
是函数 (其中
(其中 )的图像与
)的图像与 轴的交点,点
轴的交点,点 是它与
是它与 轴的一个交点,点
轴的一个交点,点 是它的一个最低点.
是它的一个最低点. 的值;
的值; ,求
,求 的值.
的值.
 中,侧棱
中,侧棱 与侧面
与侧面 的距离为2,侧面
的距离为2,侧面
 ,直线
,直线 及
及 轴所围成的图形的面积为_______
轴所围成的图形的面积为_______ 的值的程序框图,则在①、②、③处应分别填入的是( )
的值的程序框图,则在①、②、③处应分别填入的是( ) A.y=-x,y=0,y=x2
A.y=-x,y=0,y=x2 注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )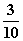 B.
B.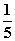 C.
C. D.
D.
 的结果是 ( )
的结果是 ( ) B. C.
B. C.  D.
D. 