题目内容
如图，在锐角三角形ABC中，D 为C在AB上的射影，E 为D在BC上的射影,F为DE上一点，且满足
(1)证明：
(2)若AD=2，CD=3.DB=4，求
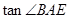的值.
(1)详见解析，(2) 
解析试题分析：(1) 设
与
交于点
，由条件
，就可找相似三角形. 
,又
，所以
，从而有△
∽△
，即
，
， (2)由(1)知
,已知
，又由条件得
,所以
，而
，所以
，从而
试题解析：
(1)证明：设与交于点,连接
.,,又△
∽△
,
.于是有,注意到
,∴△∽△,
∴,∴
四点共圆.从而有,
∴
. (5分)
(2)在
△
中, 
,
,,
,由
,知,
.又,
.
故
. (10分)
考点：相似三角形，四点共圆
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F.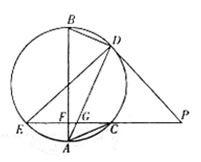
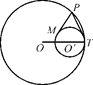
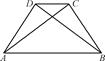
为圆
的切线,
为切点,
，
的角平分线与
和圆
和
.
（2）求
的值.
，求MA及CE的长．