题目内容
已知圆 ,以圆C与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 .
,以圆C与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 .
为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取 名学生进行问卷调查,根据问卷取得了这
名学生进行问卷调查,根据问卷取得了这 名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①
名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组① ,②
,②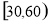 ,③
,③ ,④
,④ ,⑤
,⑤ ,⑥
,⑥ ,⑦
,⑦ ,⑧
,⑧ ,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
,得到频率分布直方图如下,已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人:
(1)求 的值并补全下列频率分布直方图;
的值并补全下列频率分布直方图;
(2)如果把“学生晚上学习时间达到两小时”作为是否充分利用时间的标准,对抽取的 名学生,完成下列
名学生,完成下列 列联表:
列联表:
利用时间充分 | 利用时间不充分 | 总计 | |
走读生 | |||
住宿生 | 10 | ||
总计 |
据此资料,你是否认为学生“利用时间是否充分”与走读、住宿有关?
参考公式:

今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
(1)求上表中的 、
、 的值,并补全下图所示的频率分布直方图;
的值,并补全下图所示的频率分布直方图;

(2)在被调查的居民中,若从年龄在 ,
, 的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.
的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.
某校高三年级文科学生600名,从参加期末考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表:
分组 | 频数 | 频率 |
[45,60) | 2 | 0.04 |
[60,75) | 4 | 0.08 |
[75,90) | 8 | 0.16 |
[90,105) | 11 | 0.22 |
[105,120) | 15 | 0.30 |
[120,135) | a | b |
[135,150] | 4 | 0.08 |
合计 | 50 | 1 |
(1)写出 的值;
的值;
(2)估计该校文科生数学成绩在120分以上学生人数;
(3)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在[135,150]中选两位同学,来帮助成绩在[45,60)中的某一位同学.已知甲同学的成绩为56分, 乙同学的成绩为145分,求甲乙在同一小组的概率.


 满足
满足 ,则
,则 的解集为( )
的解集为( ) B.
B.
 D.
D.







 ,若函数
,若函数 在区间
在区间 上有三个零点,则实数
上有三个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 中,底面ABCD为菱形,且
中,底面ABCD为菱形,且 ,
, .
.
 ;
; ,求点C到平面PBD的距离.
,求点C到平面PBD的距离. 满足
满足 且
且 ,那么它的图象是下图中的( ))
,那么它的图象是下图中的( )) B.
B. C.
C. D.
D. 若f(x)=3,则x的值是( )
若f(x)=3,则x的值是( )  B.
B. D.1,
D.1,