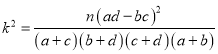题目内容
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)求函数![]() 的定义域,并求出当
的定义域,并求出当![]() 时,常数
时,常数![]() 的值;
的值;
(2)在(1)的条件下,判断函数![]() 在
在![]() 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)设![]() ,若方程
,若方程![]() 有实根,求
有实根,求![]() 的取值范围.
的取值范围.
【答案】(1)定义域为![]() 或
或![]() ,
,![]() (2)
(2)![]() 在
在![]() 的单调递增,见解析(3)
的单调递增,见解析(3)![]()
【解析】
(1)解不等式![]() 得出该函数的定义域,由
得出该函数的定义域,由![]() 结合对数的运算性质得出
结合对数的运算性质得出![]() ;
;
(2)利用定义以及不等式的性质证明单调性即可;
(3)将方程转化为二次函数,通过讨论对称轴的位置,求出![]() 的取值范围.
的取值范围.
解:(1)由![]()
![]() 且
且![]()
知![]()
∴![]() 或
或![]()
∴定义域为![]() 或
或![]()
由![]() 得
得![]()
∴![]()
∵![]()
∴![]()
(2)由(1)![]()
![]() ,判断
,判断![]() 在
在![]() 的单调递增
的单调递增
证明:设![]() ,则
,则![]()
∴![]() ,即
,即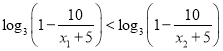
∴![]()
∴![]() 在
在![]() 的单调递增.
的单调递增.
(3)函数![]() 的定义域为
的定义域为![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,
,
∵![]() 有实根,
有实根,![]()
![]() 在
在![]() 有实根
有实根
![]()
![]() 在
在![]() 有实根
有实根
化简整理得,方程![]() 在
在![]() 上有解
上有解
设![]() 对称轴
对称轴![]() .
.
①![]() 即
即![]() 且
且![]()
∵![]() 且
且![]() 在
在![]() 为增函数,所以方程
为增函数,所以方程![]() 在
在![]() 无解.
无解.
②![]() ,即
,即![]()
则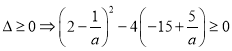 ,即
,即![]() ,解得
,解得![]()
综上![]() .
.

 考前必练系列答案
考前必练系列答案【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 | 非优秀 | 总计 |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;(把列联表自己画到答题卡上)
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
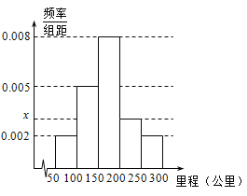
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
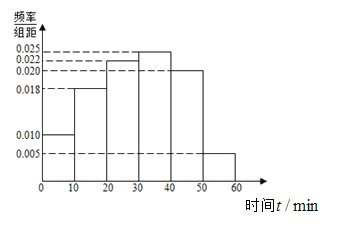
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生,已知体育健康A类学生中有10名女生.
(Ⅰ)根据已知条件完成下面![]() 列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
非体育健康A类学生 | 体育健康A类学生 | 合计 | |
男生 | |||
女生 | |||
合计 |
(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
P( | 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |