题目内容
(本小题满分14分)
当 均为正数时,称
均为正数时,称 为
为 的“均倒数”.已知数列
的“均倒数”.已知数列 的各项均为正数,且其前
的各项均为正数,且其前 项的“均倒数”为
项的“均倒数”为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设

 ,试比较
,试比较 与
与 的大小;
的大小;
(3)设函数 ,是否存在最大的实数
,是否存在最大的实数 ,使当
,使当
 时,对于一切正
时,对于一切正 整数
整数 ,都有
,都有 恒成立?
恒成立?
当
 均为正数时,称
均为正数时,称 为
为 的“均倒数”.已知数列
的“均倒数”.已知数列 的各项均为正数,且其前
的各项均为正数,且其前 项的“均倒数”为
项的“均倒数”为 .
.(1)求数列
 的通项公式;
的通项公式;(2)设


 ,试比较
,试比较 与
与 的大小;
的大小;(3)设函数
 ,是否存在最大的实数
,是否存在最大的实数 ,使当
,使当
 时,对于一切正
时,对于一切正 整数
整数 ,都有
,都有 恒成立?
恒成立?解:(1) 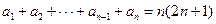 ,
,
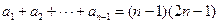 ,两式相减,得
,两式相减,得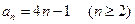 .
.
又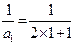 ,解得
,解得 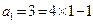 ,∴
,∴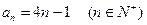 ….…4分
….…4分
(2)∵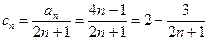 ,
,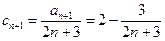 ,
,
∴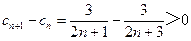 , 即
, 即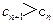 . ……………………8分
. ……………………8分
(3)由(2)知数列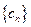 是单调递增数列,
是单调递增数列,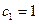 是其的最小项,
是其的最小项,
即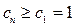 .……………………………………………………………9分
.……………………………………………………………9分
假设存在最大实数,使当 时,对于一切正整
时,对于一切正整 数
数 ,
,
都有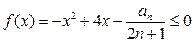 恒成立,……………………11分
恒成立,……………………11分
则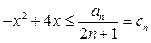
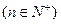 .只需
.只需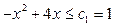 , ………12分
, ………12分
即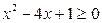 .解之得
.解之得
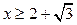 或
或 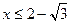 .
.
于是,可取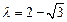 ………………………………………………………14分
………………………………………………………14分
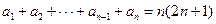 ,
,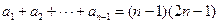 ,两式相减,得
,两式相减,得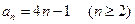 .
.又
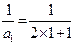 ,解得
,解得 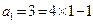 ,∴
,∴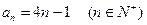 ….…4分
….…4分 (2)∵
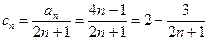 ,
,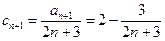 ,
, ∴
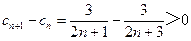 , 即
, 即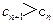 . ……………………8分
. ……………………8分(3)由(2)知数列
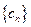 是单调递增数列,
是单调递增数列,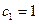 是其的最小项,
是其的最小项,即
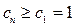 .……………………………………………………………9分
.……………………………………………………………9分假设存在最大实数,使当
 时,对于一切正整
时,对于一切正整 数
数 ,
,都有
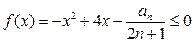 恒成立,……………………11分
恒成立,……………………11分则
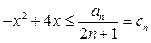
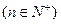 .只需
.只需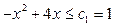 , ………12分
, ………12分即
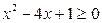 .解之得
.解之得
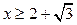 或
或 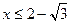 .
.于是,可取
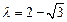 ………………………………………………………14分
………………………………………………………14分略

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
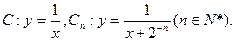 从C上一点Qn(xn,yn)作x轴的垂线,交Cn于点Pn,再从点Pn作y轴的垂线,交C于点Qn+1(xn+1,yn+1)。设x1=1,an=xn+1-xn,bn=yn-yn+1
从C上一点Qn(xn,yn)作x轴的垂线,交Cn于点Pn,再从点Pn作y轴的垂线,交C于点Qn+1(xn+1,yn+1)。设x1=1,an=xn+1-xn,bn=yn-yn+1 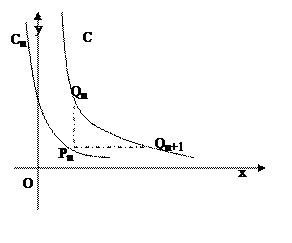 ③记数列{an·bn}的前n项和为Sn,求证:
③记数列{an·bn}的前n项和为Sn,求证: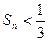
 }的前n项和为
}的前n项和为 ,且
,且 。
。 ,求数列{
,求数列{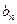 }的前n项和
}的前n项和 。
。 满足
满足 为常数,则其前( )项的和也是常数。
为常数,则其前( )项的和也是常数。 其中
其中 为预测期内年增长率,
为预测期内年增长率,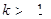 ,
, 为预测期人口数,
为预测期人口数, 为初期人口数,
为初期人口数,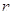 为预测期间隔年数。如果在某一时期有
为预测期间隔年数。如果在某一时期有 ,那么在这期间人口数
,那么在这期间人口数 .,写出它的前5项,并归纳出数列的一个通项公式
.,写出它的前5项,并归纳出数列的一个通项公式 (不要求证明)
(不要求证明)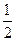 +
+ 的图象上的任意两点,且
的图象上的任意两点,且 =
= ),已知点M的横坐标为
),已知点M的横坐标为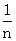 )+f(
)+f( )+…+f(
)+…+f( ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn; . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn< (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数 的四个实根组成以
的四个实根组成以 为首项的等差数列,则
为首项的等差数列,则 
 C.
C. D.
D.
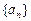 中,
中, 前5项和
前5项和 则其公差
则其公差