题目内容
如图 △ABC内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D.
△ABC内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D.(I)求证:AC2=AP•AD;
(II)若∠ABC=60°,⊙O的半径为1,且P为弧AC的中点,求AD的长.
分析:(I)根据三角形中两条边相等,得到对应的两个底角相等,证明两个三角形相似,相似三角形对应边成比例,得到比例式,通过等量代换得到要求的等式.
(II)根据有一个顶角是60°的等腰三角形是等边三角形,得到∠BAC=60°,从而得到∠BAP=90°,即BP是圆的直径,在直角三角形中利用勾股定理得到结果.
(II)根据有一个顶角是60°的等腰三角形是等边三角形,得到∠BAC=60°,从而得到∠BAP=90°,即BP是圆的直径,在直角三角形中利用勾股定理得到结果.
解答:(I)证明:连接BP,
∵AB=AC,
∴∠ABC=∠ACB又∠ACB=∠APB,
∴∠ABC=∠APB,
∴△ABP∽△ABD
∴
=
即AB2=AP•AD,
∵AB=AC,
∴AC2=AP•AD
(II)∵∠ABC=60°,AB=AC,
∴△ABC是等边三角形,
∴∠BAC=60°,
∵P为为弧AC的中点,
∴∠ABP=∠PAC=30°,
∴∠BAP=90°,
∴BP是圆的直径,
∴BP=2,
∴AP=
BP=1,
在直角三角形PAB中,AB2=BP2-AP2=3,
∴AD=
=3
∵AB=AC,
∴∠ABC=∠ACB又∠ACB=∠APB,
∴∠ABC=∠APB,
∴△ABP∽△ABD
∴
| AB |
| AP |
| AD |
| AB |
∵AB=AC,
∴AC2=AP•AD
(II)∵∠ABC=60°,AB=AC,
∴△ABC是等边三角形,
∴∠BAC=60°,
∵P为为弧AC的中点,
∴∠ABP=∠PAC=30°,
∴∠BAP=90°,
∴BP是圆的直径,
∴BP=2,
∴AP=
| 1 |
| 2 |
在直角三角形PAB中,AB2=BP2-AP2=3,
∴AD=
| AB2 |
| AP |
点评:本题考查与圆有关的比例线段,考查三角形相似和全等的判断和性质的应用,本题是一个综合题目,解题时注意题目所给的条件比较繁琐,不要用错条件.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
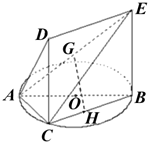 如图△ABC内接于圆O,G,H分别是AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.证明:
如图△ABC内接于圆O,G,H分别是AE,BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.证明: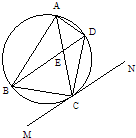 (2012•吉林二模)如图△ABC内接于圆O,AB=AC,直线MN切圆O于点C,BD∥MN,AC与BD相交于点E.
(2012•吉林二模)如图△ABC内接于圆O,AB=AC,直线MN切圆O于点C,BD∥MN,AC与BD相交于点E.
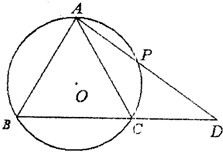 △ABC内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D.
△ABC内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D.