Question

【题目】已知椭圆 =1（a＞b＞0）的一个顶点为A（0，1），离心率为 ，过点B（0，﹣2）及左焦点F1的直线交椭圆于C，D两点，右焦点设为F2 ．
（1）求椭圆的方程；
（2）求△CDF2的面积．

Answer 1

【答案】
（1）解：∵椭圆 =1（a＞b＞0）的一个顶点为A（0，1），离心率为 ，

∴b= =1，且 = ，解之得a= ，c=1

可得椭圆的方程为

（2）解：∵左焦点F1（﹣1，0），B（0，﹣2），得F1B直线的斜率为﹣2

∴直线F1B的方程为y=﹣2x﹣2

由 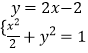，化简得9x2+16x+6=0．

∵△=162﹣4×9×6=40＞0，

∴直线与椭圆有两个公共点，设为C（x1，y1），D（x2，y2），

则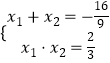

∴|CD|= |x1x2|= = =

又∵点F2到直线BF1的距离d= = ，

∴△CDF2的面积为S= |CD|×d= × =

【解析】（1）根据椭圆的基本概念和平方关系，建立关于a、b、c的方程，解出a= ，b=c=1，从而得到椭圆的方程；（2）求出F1B直线的斜率得直线F1B的方程为y=﹣2x﹣2，与椭圆方程联解并结合根与系数的关系算出|xspan>1﹣x2|= ，结合弦长公式可得|CD|= ，最后利用点到直线的距离公式求出F2到直线BF1的距离d，即可得到△CDF2的面积．