题目内容
若周期为2的函数f(x)满足当x∈[1,3]时,f(x)=
,且f(2)=f(
),则ab的值为
|
| 9 |
| 4 |
24
24
.分析:观察所给函数的解析式,结合条件周期为2,可以得到f(1)=f(3),再利用f(2)=f(
),两个条件构成方程组求解出a与b,再求ab.
| 9 |
| 4 |
解答:解:因为函数f(x)的周期为2,所以f(1)=f(3),
即2+b=3a+1 ①
又f(2)=f(
),所以4+b=
a+1 ②
由①②联立可求得a=-
,b=-9,
所以ab=24,
故答案为24.
即2+b=3a+1 ①
又f(2)=f(
| 9 |
| 4 |
| 9 |
| 4 |
由①②联立可求得a=-
| 8 |
| 3 |
所以ab=24,
故答案为24.
点评:解决该问题的突破口在所给函数的定义域的区间长度与周期相同.

练习册系列答案
相关题目
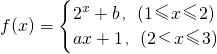 ,且
,且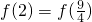 ,则ab的值为________.
,则ab的值为________.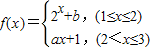 ,且
,且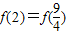 ,则ab的值为 .
,则ab的值为 .