题目内容
已知椭圆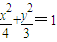 ,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1,F2距离的等差中项,若能找到,求出该点的坐标,若不能找到,请说明理由.
,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1,F2距离的等差中项,若能找到,求出该点的坐标,若不能找到,请说明理由.
【答案】分析:过点M作左准线的垂线MA交左准线于A,由M点到左准线的距离为它到两焦点F1,F2距离的等差中项知2|MA|=|MF1|+|MF2|,此结合题设条件能够推导出|MA|=2,从而导出M点的坐标.
解答:解:在椭圆 位于y轴左侧的部分上有一点M,它到左准线的距离为它到两焦点F1,F2距离的等差中项.
位于y轴左侧的部分上有一点M,它到左准线的距离为它到两焦点F1,F2距离的等差中项.
过点M作左准线的垂线MA交左准线于A,则2|MA|=|MF1|+|MF2|.
∵ ,
,
∴2|MF1|=|MA|+2-|MF1|,
∴3|MF1|=|MA|+2,
∴ ,
,
∴
∴|MA|=2.
∵点A在左准线x=-4上,
∴M点的横坐标x=-4+2=-2.
把x=-2代入椭圆 得y=0,∴M(-2,0).
得y=0,∴M(-2,0).
故存在点M,其坐标是M(-2,0).
点评:本题考查椭圆的基础知识,解题时注意挖掘隐含条件.
解答:解:在椭圆
 位于y轴左侧的部分上有一点M,它到左准线的距离为它到两焦点F1,F2距离的等差中项.
位于y轴左侧的部分上有一点M,它到左准线的距离为它到两焦点F1,F2距离的等差中项.过点M作左准线的垂线MA交左准线于A,则2|MA|=|MF1|+|MF2|.
∵
 ,
,∴2|MF1|=|MA|+2-|MF1|,
∴3|MF1|=|MA|+2,
∴
 ,
,∴

∴|MA|=2.
∵点A在左准线x=-4上,
∴M点的横坐标x=-4+2=-2.
把x=-2代入椭圆
 得y=0,∴M(-2,0).
得y=0,∴M(-2,0).故存在点M,其坐标是M(-2,0).
点评:本题考查椭圆的基础知识,解题时注意挖掘隐含条件.

练习册系列答案
相关题目
 ,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1,F2距离的等差中项,若能找到,求出该点的坐标,若不能找到,请说明理由.
,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1,F2距离的等差中项,若能找到,求出该点的坐标,若不能找到,请说明理由.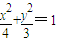 ,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1,F2距离的等差中项,若能找到,求出该点的坐标,若不能找到,请说明理由.
,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1,F2距离的等差中项,若能找到,求出该点的坐标,若不能找到,请说明理由.