题目内容

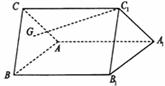
如图，斜三棱柱ABC―A1B1C1中，侧面ACC1A1⊥侧面ABB1A­1，AC=AB=，∠CAA1=∠BAA1=135°。

   （Ⅰ）求∠BAC的大小。

   （Ⅱ）若底面△ABC重心为G，侧棱AA1=4，求GC1与平面A1B1C1所成角的大小。

解：作CO⊥AA1交A1A的延长线于点O，连接BO。

    则CO⊥平面ABB1A1。

    易证△OAC≌BAO，∴BO⊥AA1

   （Ⅰ）由cos∠CAB= cos∠OAC?cos∠OAB，

    知cos∠CAB= cos245°=

    ∴∠CAB= 60°。

   （Ⅱ）以O为坐标原点，建立如图所示的空间直角坐标系

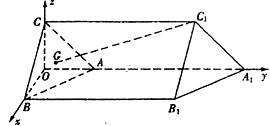
    则A（0，1，0），B（1，0，0），C（0，0，1）

   

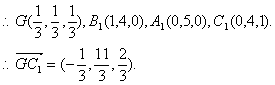
设平面A1B1C1的法向量为

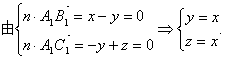
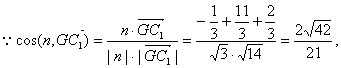
练习册系列答案
相关题目
精英家教网已知如图，斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，∠ABC=90°，BC=2，AC=2
3
，且AA1⊥A1C，AA1=A1C．
（1）求侧棱A1A与底面ABC所成角的大小；
（2）求侧面A1ABB1与底面ABC所成二面角的大小；
（3）求顶点C到侧面A1ABB1的距离．
精英家教网如图，斜三棱柱ABC-A1B1C1中，A1C1⊥BC1，AB⊥AC，AB=3，AC=2，侧棱与底面成60°角．
（1）求证：AC⊥面ABC1；
（2）求证：C1点在平面ABC上的射影H在直线AB上；
（3）求此三棱柱体积的最小值．
精英家教网如图，斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
3
2
的菱形，∠ACC1为锐角，侧面ABB1A1⊥侧面AA1C1C，且A1B=AB=AC=1．
（Ⅰ）求证：AA1⊥BC1；
（Ⅱ）求三棱锥A1-ABC的体积．
如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，AC⊥CB，∠ABC=45°，侧面A1ABB1是边长为a的菱形，且垂直于底面ABC，∠A1AB=60°，E、F分别是AB1、BC的中点．
（1）求证EF∥平面A1ACC1；
（2）求EF与侧面A1ABB1所成的角．
（2012•潍坊二模）如图，斜三棱柱ABC-A1B1C1，侧面BB1C1C⊥底面ABC，△BC1C是等边三角形，AC⊥BC，AC=BC=4．
（1）求证：AC⊥B
C
 
1
；
（2）设D为BB1的中点，求二面角D-AC-B的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网