题目内容
把长为12 cm的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是
- A.
cm2 - B.4cm2
- C.3
cm2 - D.2cm2
D
分析：设两段长分别为xcm，（12-x）cm，则这两个正三角形面积之和 S=
（
）2 +（
）2，
利用二次函数的性质求出其最小值．
解答：设两段长分别为xcm，（12-x）cm，
则这两个正三角形面积之和 S=（）2 +（）2
=
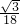（x2-12x+72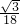）=[（x-6）2+36]≥2，
故选 D．
点评：本题考查等边三角形的面积的求法，二次函数的性质及最小值的求法．
分析：设两段长分别为xcm，（12-x）cm，则这两个正三角形面积之和 S=
（）2 +（）2，利用二次函数的性质求出其最小值．
解答：设两段长分别为xcm，（12-x）cm，
则这两个正三角形面积之和 S=
（）2 +（）2=
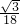（x2-12x+72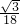）=[（x-6）2+36]≥2，故选 D．
点评：本题考查等边三角形的面积的求法，二次函数的性质及最小值的求法．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
cm2
cm2
cm2
cm2 B.4cm2 C.
cm2 D.
cm2
cm2 B.4 cm2
cm2 D.2
cm2