题目内容
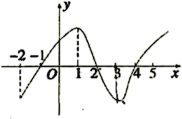
【题目】如图是
的导函数
的图象，对于下列四个判断，其中正确的判断是（ ）.
A.
在
上是增函数；
B.当
时，取得极小值；
C.在
上是增函数、在
上是减函数；
D.当
时，取得极大值.
【答案】BC
【解析】
这是一个图象题，考查了两个知识点：①导数的正负与函数单调性的关系，若在某个区间上，导数为正，则函数在这个区间上是增函数，若导数为负，则这个函数在这个区间上是减函数；②极值判断方法，在导数为零的点处左增右减取到极大值，左减右增取到极小值．
解：由图象可以看出，在
，
上导数小于零，故
不对；
左侧导数小于零，右侧导数大于零，所以是
的极小值点,故
对；
在
，
上导数大于零，在
上导数小于零，故
对；
左右两侧导数的符号都为正，所以不是极值点，
不对．
故选：BC．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
